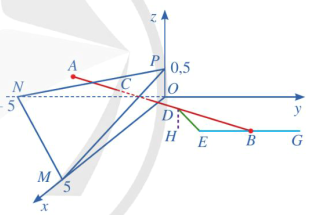
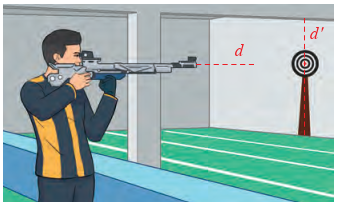
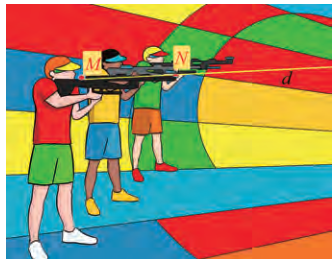
Trên phần mềm mô phỏng 3 D một máy khoan trong không gian Oxyz, cho biết phương trình trục \(a\) của mũi khoan và một đường rãnh \(b\) trên vật cần khoan (Hình 18) lần lượt là:
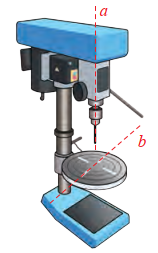
a) Chứng minh a và b vuông góc và cắt nhau.
b) Tìm giao điểm của \(a\) và \(b\).
Trên phần mềm mô phỏng 3 D một máy khoan trong không gian Oxyz, cho biết phương trình trục \(a\) của mũi khoan và một đường rãnh \(b\) trên vật cần khoan (Hình 18) lần lượt là:

a) Chứng minh a và b vuông góc và cắt nhau.
b) Tìm giao điểm của \(a\) và \(b\).
Quảng cáo
Trả lời:
a) Đường thắng a đi qua \({\rm{M}}(1;2;0)\) và có vectơ chí phương là \(\vec a = (0;0;3)\) Đường thắng b đi qua \({\rm{N}}(1;2;6)\) và có vectơ chí phương \(\overrightarrow {{a^\prime }} = (4;2;0)\) Có \(\vec a \cdot \overrightarrow {{a^\prime }} = 0.4 + 0.2 + 3.0 = 0\). Suy ra a \( \bot {\rm{b}}\).
Ta xét hệ \(\left\{ {\begin{array}{*{20}{l}}{1 = 1 + 4{t^\prime }}\\{2 = 2 + 2{t^\prime }}\\{3t = 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{t^\prime } = 0}\\{{t^\prime } = 0.{\rm{ }}}\\{t = 2}\end{array}} \right.} \right.\)Suy ra hệ có nghiệm duy nhất. Do đó a và b cắt nhau.
b) Thay \({\rm{t}} = 2\) vào phương trình đường thắng a ta được \(\left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = 2}\\{z = 6}\end{array}} \right.\)
Vậy tọa độ giao điếm của hai đường thắng này là \((1;2;6)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
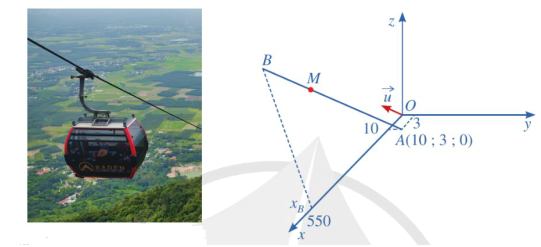
a) Phương trình chính tắc của đường cáp là: \(\frac{{x - 10}}{2} = \frac{{y - 3}}{{ - 2}} = \frac{z}{1}\).
b) Do tốc độ chuyển động của cabin là \(4,5\;{\rm{m}}/{\rm{s}}\) nên độ dài AM bằng \(4,5t(\;{\rm{m}})\). Vì vậy \(|\overrightarrow {AM} | = 4,5t(t \ge 0)\).
Do hai vectơ \(\overrightarrow {AM} \) và \(\vec u\) là cùng phương và cùng hướng nên \(\overrightarrow {AM} = k\vec u\) với \(k\) là số thực dương nào đó. Suy ra: \(|\overrightarrow {AM} | = k|\vec u| = k \cdot \sqrt {{2^2} + {{( - 2)}^2} + 1} = 3k\). Do đó \(3k = 4,5t\). Suy ra \(k = \frac{{3t}}{2}\). Vì thế, ta có: \(\overrightarrow {AM} = \frac{{3t}}{2}\vec u = \left( {3t; - 3t;\frac{{3t}}{2}} \right)\).
Gọi toạ độ của điểm \(M\) là \(\left( {{x_M};{y_M};{z_M}} \right)\).
Do \(\overrightarrow {AM} = \left( {{x_M} - {x_A};{y_M} - {y_A};{z_M} - {z_A}} \right) = \left( {3t; - 3t;\frac{{3t}}{2}} \right)\) nên \(\left\{ {\begin{array}{*{20}{l}}{{x_M} = 3t + {x_A}}\\{{y_M} = - 3t + {y_A}}\\{{z_M} = \frac{{3t}}{2} + {z_A}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_M} = 3t + 10}\\{{y_M} = - 3t + 3}\\{{z_M} = \frac{{3t}}{2}.}\end{array}} \right.} \right.\)
Vậy điểm \(M\) có toạ độ là \(\left( {3t + 10; - 3t + 3;\frac{{3t}}{2}} \right)\).
c) Do \({x_B} = 550\) nên \(3t + 10 = 550\), tức là \(t = 180\) (s). Do đó, ta có điểm \(B(550; - 537;270)\).
Vậy \(AB = \sqrt {{{(550 - 10)}^2} + {{( - 537 - 3)}^2} + {{(270 - 0)}^2}} = \sqrt {656100} = 810(\;{\rm{m}})\).
d) Đường thẳng AB có vectơ chỉ phương \(\vec u = (2; - 2;1)\) và mặt phẳng (Oxy) có vectơ pháp tuyếnLời giải
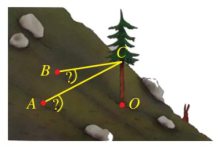
a) Do điểm \(C(0;0;5)\) nên \(AC = \sqrt {{{(3 - 0)}^2} + {{( - 4 - 0)}^2} + {{(2 - 5)}^2}} = \sqrt {34} (\;{\rm{m}})\);
\(BC = \sqrt {{{( - 5 - 0)}^2} + {{( - 2 - 0)}^2} + {{(1 - 5)}^2}} = \sqrt {45} = 3\sqrt 5 (\;{\rm{m}}){\rm{. }}\)
b) Ta có: \(\overrightarrow {OA} = (3; - 4;2),\overrightarrow {OB} = ( - 5; - 2;1)\) nên \([\overrightarrow {OA} ,\overrightarrow {OB} ] = \left( {\left| {\begin{array}{*{20}{l}}{ - 4}&2\\{ - 2}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}2&3\\1&{ - 5}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}3&{ - 4}\\{ - 5}&{ - 2}\end{array}} \right|} \right) = (0; - 13; - 26){\rm{. }}\)
Vì thế, vectơ \(\vec n = (0;1;2)\) là một vectơ pháp tuyến của mặt phẳng \((OAB)\).
Mặt khác, do \(\overrightarrow {CA} = (3; - 4; - 3),\overrightarrow {BC} = (5;2;4)\) nên ta có:
- \(\sin (CA,(OAB)) = |\cos (\overrightarrow {CA} ,\vec n)| = \frac{{|\overrightarrow {CA} \cdot \vec n|}}{{|\overrightarrow {CA} | \cdot |\vec n|}} = \frac{{|3 \cdot 0 + ( - 4) \cdot 1 + ( - 3) \cdot 2|}}{{\sqrt {34} \cdot \sqrt 5 }} = \frac{{10}}{{\sqrt {170} }}\),
suy ra . Vậy góc tạo bởi dây neo CA và mặt phẳng sườn núi là khoảng .
suy ra . Vậy góc tạo bởi dây neo BC và mặt phẳng sườn núi là khoảng .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.