Cho bát giác đều \(ABCDEFGH\) nội tiếp đường tròn tâm \[O\]. Phép quay thuận chiều \(135^\circ \) biến hình tam giác \(OAB\) thành tam giác nào?
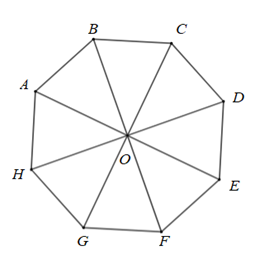
Cho bát giác đều \(ABCDEFGH\) nội tiếp đường tròn tâm \[O\]. Phép quay thuận chiều \(135^\circ \) biến hình tam giác \(OAB\) thành tam giác nào?
A. \(\Delta OBC\).
B. \(\Delta OCD\).
C. \(\Delta ODE\).
D. \(\Delta OEA\).
Câu hỏi trong đề: 35 bài tập Đa giác đều. Phép quay có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn B
Ta có \(ABCDEFGH\) là hình bát giác đều nên \(AB = BC = CD = DE = EF = FG = GH = HA\).
Suy ra số đo các cung nhỏ \(AB\), \(BC\), \(CD\), \[DE\], \(EF\), \(FG\), \(GH\), \(HA\) đều bằng \(\frac{{360^\circ }}{8} = 45^\circ \).
Do đó phép quay thuận chiều \(135^\circ \) tâm \(\left( O \right)\) biến điểm \(A\) thành điểm \(F\), điểm \(B\) thành điểm \(G\), điểm \(O\) thành điểm \(O\).
Vậy phép quay thuận chiều \(135^\circ \) biến tam giác \[OAB\] thành tam giác \(\Delta OFG\).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn A
Câu 2
A. phép quay thuận chiều \(90^\circ \)tâm \[O\].
B. phép quay thuận chiều \(180^\circ \)tâm \[O\].
C. Phép ngược chiều \(90^\circ \)tâm \[O\].
D. phép thuận chiều \(120^\circ \) tâm \[O\].
Lời giải
Chọn D
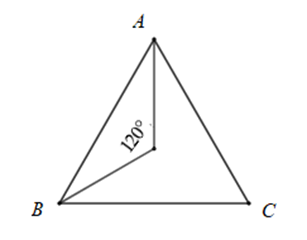
Ta có \(\Delta ABC\) là tam giác đều nên \[AB = BC = CA\]
Do đó sđsđ\( = \)sđ .
Vậy các phép quay thuận chiều (hoặc ngược chiều) \(0^\circ \), \(120^\circ \), \(240^\circ \), \(360^\circ \) tâm \[O\] giữ nguyên hình \(\Delta ABC\)
Câu 3
A. \(5\).
B. \(4\).
C. \(3\).
D. \(2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(5\).
B. \(4\).
C. \(3\).
D. \(6\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(240^\circ \).
B. \(120^\circ \).
C. \(90^\circ \).
D. \(45^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Điểm \[A\].
B. Điểm \[B\].
C. Điểm.
D. Điểm \[O\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Điểm \[A\].
B. Điểm \[B\].
C. Điểm \[D\].
D. Điểm \[C\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập