Cho tứ giác \(ABCD\) nội tiếp đường tròn, biết \[\widehat A = 100^\circ ,\,\,\widehat B = 70^\circ \]. Vậy số đo\[\widehat C\] & \[\widehat D\] bằng:
A. \[\widehat C = 80^\circ ;\,\,\widehat D = 100^\circ \]
B. \[\widehat C = 80^\circ ;\,\,\widehat D = 70^\circ \]
C. \[\widehat C = 80^\circ ;\,\,\widehat D = 140^\circ \]
D. \[\widehat C = 80^\circ ;\,\,\widehat D = 110^\circ \]
Câu hỏi trong đề: 39 bài tập Tứ giác nội tiếp có lời giải !!
Quảng cáo
Trả lời:
Chọn D
Vì tứ giác \(ABCD\) nội tiếp, ta có: \[\widehat A + \widehat C = 180^\circ \](theo định lí) \[ \Rightarrow \widehat C = 80^\circ \]
\[\widehat B + \widehat D = 180^\circ \](theo định lí) \[ \Rightarrow \widehat D = 110^\circ \]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[20^\circ .\]
B.
C. \[30^\circ .\]
D. \[40^\circ .\]
Lời giải
Chọn A
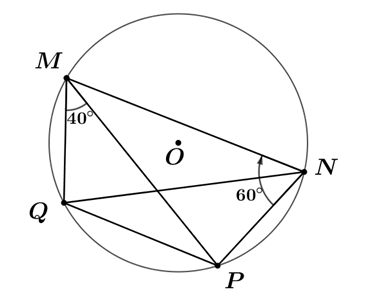
Tứ giác \(MNPQ\) nội tiếp \( \Rightarrow \widehat {MQP\,} = \,180^\circ - \,\widehat {MNP} = \,120^\circ \).
(Định lí tổng ba góc trong một tam giác).
Câu 2
A. \[45^\circ \]
B. \[90^\circ \]
C. \[125^\circ \]
D. \[135^\circ \].
Lời giải
Chọn D
Tứ giác \[MNPQ\] có\[\widehat {PMQ} = \widehat {PNQ} = 90^\circ \]\( \Rightarrow \) Tứ giác \[MNPQ\] nội tiếp đường tròn đường kính \(PQ\)
\( \Rightarrow \widehat {MQP}\, + \,\widehat {MNP\,} = 180^\circ \). (1)
\(\Delta MPQ\) vuông tại \(M\) (gt) và \(MP = \,MQ\) (gt) \( \Rightarrow \Delta MPQ\) vuông cân tại \(M \Rightarrow \widehat {MQP}\, = \,45^\circ \). (2)
Từ (1), (2) suy ra: \(\widehat {MNP\,} = \,135^\circ \).
Câu 3
A. \[120^\circ \]
B. \[40^\circ \]
C. \[20^\circ \]
D. \[60^\circ \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[40^\circ \]
B. \[50^\circ \]
C. \[90^\circ \]
D. \[10^\circ \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[40^\circ \]
B. \[50^\circ \]
C. \[90^\circ \]
D. \[60^\circ \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[60^\circ \] hoặc \[120^\circ .\]
B. \[80^\circ .\]
C. \[100^\circ \]
D. \[120^\circ \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Tứ giác \[ABCD\] là tứ giác nội tiếp.
B. Tứ giác \[ABCD\] không nội tiếp được.
C. Tứ giác \[ABCD\] là một hình thoi.
D. Tứ giác \[ABCD\] là một hình thang cân.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.