Cho đường tròn \(\left( O \right)\) đường kính \(AB\). Gọi \(H\) là điểm nằm giữa \(O\) và \(B\). Kẻ dây \(CD \bot AB\) tại \(H\). Trên cung nhỏ \(AC\) lấy điểm \(E\), kẻ \(CK \bot AE\) tại \(K\). Đường thẳng \(DE\) cắt \(CK\) tại \(F\). Tam giác \(ACF\) là tam giác
A. cân tại \(F\).
B. cân tại \(C\).
C. cân tại \(A\).
D. đều.
Câu hỏi trong đề: 39 bài tập Tứ giác nội tiếp có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn C
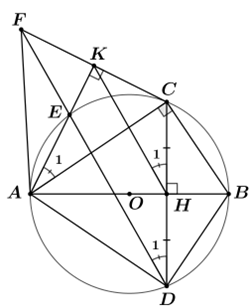
Ta có \(AB \bot CD\) tại \(H\) mà \(AB\) là đường kính suy ra \(H\) là trung điểm của \(CD\). (1)
Trên \(\left( O \right)\): \(\widehat {{A_1}}\, = \,\widehat {{D_1}}\) (góc nội tiếp cùng chắn ). (2)
Dễ dàng, chứng minh được tứ giác \(AHCK\) nội tiếp đường tròn đường kính \(AC\).
Suy ra \(\widehat {{A_1}}\, = \,\widehat {{H_1}}\) (góc nội tiếp cùng chắn ). (3)
Từ (2), (3) suy ra \(\widehat {{D_1}\,} = \,\widehat {{H_1}}\) mà \(\widehat {{D_1}\,};\,\widehat {{H_1}}\) là cặp góc nằm ở vị trí đồng vị \( \Rightarrow \)HK //\(DF\). (4)
Từ (1), (4) suy ra \(K\) là trung điểm của \(FC\).
hay \(AK\) là đường trung tuyến xuất phát từ đỉnh \(A\) của \(\Delta AFC\).
mà \(AK\) cũng là đường cao xuất phát từ đỉnh \(A\) của \(\Delta AFC\).
Do đó: \(\Delta ACF\) cân tại \(A\).
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[20^\circ .\]
B.
C. \[30^\circ .\]
D. \[40^\circ .\]
Lời giải
Chọn A
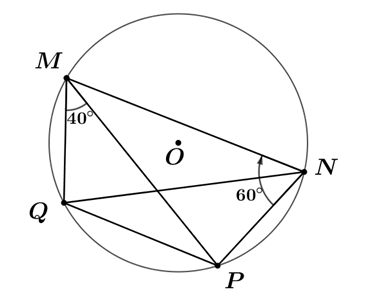
Tứ giác \(MNPQ\) nội tiếp \( \Rightarrow \widehat {MQP\,} = \,180^\circ - \,\widehat {MNP} = \,120^\circ \).
(Định lí tổng ba góc trong một tam giác).
Câu 2
A. \[45^\circ \]
B. \[90^\circ \]
C. \[125^\circ \]
D. \[135^\circ \].
Lời giải
Chọn D
Tứ giác \[MNPQ\] có\[\widehat {PMQ} = \widehat {PNQ} = 90^\circ \]\( \Rightarrow \) Tứ giác \[MNPQ\] nội tiếp đường tròn đường kính \(PQ\)
\( \Rightarrow \widehat {MQP}\, + \,\widehat {MNP\,} = 180^\circ \). (1)
\(\Delta MPQ\) vuông tại \(M\) (gt) và \(MP = \,MQ\) (gt) \( \Rightarrow \Delta MPQ\) vuông cân tại \(M \Rightarrow \widehat {MQP}\, = \,45^\circ \). (2)
Từ (1), (2) suy ra: \(\widehat {MNP\,} = \,135^\circ \).
Câu 3
A. \[40^\circ \]
B. \[50^\circ \]
C. \[90^\circ \]
D. \[60^\circ \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[AC = AB\]
B. \[AC = BD\]
C. \[DB = AB\]
D. Không có đáp án đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[24^\circ .\]
B. \[29^\circ .\]
C. \[30^\circ .\]
D. \[31^\circ .\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Tứ giác \[ABCD\] là tứ giác nội tiếp.
B. Tứ giác \[ABCD\] không nội tiếp được.
C. Tứ giác \[ABCD\] là một hình thoi.
D. Tứ giác \[ABCD\] là một hình thang cân.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[120^\circ \]
B. \[40^\circ \]
C. \[20^\circ \]
D. \[60^\circ \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo