Cho tứ giác \[ABCD\] nội tiếp đường tròn tâm \(O\) bán kính \[a\]. Biết rằng \[AC \bot BD\]. Khi đó để\[AB + CD\] đạt giá trị lớn nhất thì
A. \[AC = AB\]
B. \[AC = BD\]
C. \[DB = AB\]
D. Không có đáp án đúng.
Câu hỏi trong đề: 39 bài tập Tứ giác nội tiếp có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn B
![Cho tứ giác ABCD nội tiếp đường tròn tâm O bán kính a . Biết rằng AC \bot BD\]. Khi đó để\[AB + CD\] đạt giá trị lớn nhất thì (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/08/blobid25-1755533050.png)
Vẽ đường kính \(CE\) của đường tròn \(\left( O \right)\).
Ta có \(\widehat {EAC} = 90^\circ \), \(\widehat {EDC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
Từ đó ta có \(AE \bot AC\). Mặt khác theo giả thiết \(AC \bot BD\).
Kéo theo \(AE{\rm{ // }}BD\). Vậy \(AEBD\)là hình thang.
Do hình thang \[AEBD\] nội tiếp đường tròn \(\left( O \right)\) nên \(AEDB\) là hình thang cân.
Kéo theo \(AB = DE\) (các cạnh bên của hình thang).
Từ đó ta có \[A{B^2} + C{D^2} = D{E^2} + D{C^2} = E{C^2} = {\left( {2a} \right)^2} = 4{a^2}\] (do \(\Delta EDC\) vuông tại \(D\)).
Áp dụng bất đẳng thức Cauchy cho \(\left( {A{B^2},C{D^2}} \right)\) ta có \(A{B^2} + C{D^2} \ge 2AB.CD\)
\( \Rightarrow 2\left( {A{B^2} + C{D^2}} \right) \ge A{B^2} + C{D^2} + 2AB.CD = {\left( {AB + CD} \right)^2}\).
Kéo theo \({\left( {AB + CD} \right)^2} \le 2{\left( {4a} \right)^2} = 8{a^2}\)\( \Rightarrow AB + CD \le 2\sqrt 2 a\).
Đẳng thức xảy ra khi và chỉ khi\[AB = CD\].
Xét \(\Delta ABI\), \(\Delta DCI\) có \(AB = CD\), \(\widehat {ABD} = \widehat {ACD}\) (góc nội tiếp cùng chắn ),
\(\widehat {BAC} = \widehat {CDB}\) (góc nội tiếp cùng chắn ).
Do đó \(\Delta ABI = \)\(\Delta DCI\) (g.c.g).
Kéo theo \(AI = ID,IB = IC\).
Suy ra \(AC = AI + IC = ID + IB = BD\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[20^\circ .\]
B.
C. \[30^\circ .\]
D. \[40^\circ .\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn A
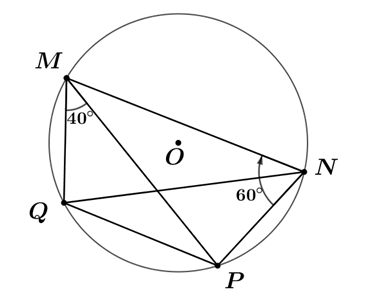
Tứ giác \(MNPQ\) nội tiếp \( \Rightarrow \widehat {MQP\,} = \,180^\circ - \,\widehat {MNP} = \,120^\circ \).
(Định lí tổng ba góc trong một tam giác).
Câu 2
A. \[120^\circ \]
B. \[40^\circ \]
C. \[20^\circ \]
D. \[60^\circ \]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn A
Tứ giác \(ABCD\) nội tiếp \(\left( O \right)\)\( \Rightarrow \widehat {{D_1}}\, = \,\widehat {{B_1}}\,\)
\(\widehat {{A_1}}\, = \,\widehat {{A_2}}\) (hai góc đối đỉnh).
\(\widehat {{D_1}}\, = \,180^\circ \, - \,\widehat {{A_1}} - \,\widehat {M\,}\, = \,160^\circ - \,\widehat {{A_1}}\).
\(\widehat {{B_1}}\, = \,40\,^\circ \, + \,\widehat {{A_2}}\,\)(Góc ngoài tại đỉnh \(B\) của \(\Delta ABN\))\( \Rightarrow \widehat {{D_1}} = \,40^\circ + \,\widehat {{A_1}}\).
Do đó: \(160^\circ - \widehat {{A_1}}\, = \,40^\circ + \,\widehat {{A_1}} \Rightarrow \widehat {{A_1}} = \,60^\circ \Rightarrow \widehat {BAD} = \,120^\circ \).
Câu 3
A. \[45^\circ \]
B. \[90^\circ \]
C. \[125^\circ \]
D. \[135^\circ \].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[40^\circ .\]
B. \[70^\circ .\]
C. \[60^\circ .\]
D. \[50^\circ .\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[40^\circ \]
B. \[50^\circ \]
C. \[90^\circ \]
D. \[60^\circ \]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[40^\circ \]
B. \[50^\circ \]
C. \[90^\circ \]
D. \[10^\circ \]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[100^\circ \]
B. \[95^\circ \]
C. \[80^\circ \]
D. \[90^\circ \]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập