(2,0 điểm)

1) Biểu đồ đoạn thẳng biểu diễn tổng thu nhập của người lao động Việt Nam trong sản xuất thiết bị điện qua các năm 2017; 2018; 2019; 2020.

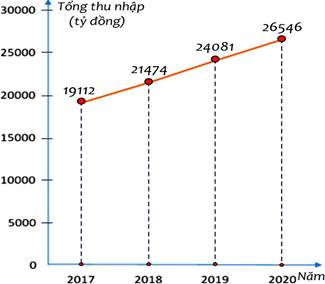
(Nguồn: Niên giám thống kê 2021)

a) Lập bảng thống kê tổng thu nhập của người lao động Việt Nam trong sản xuất thiết bị điện qua các năm trên theo mẫu sau đơn vị (tỷ đồng):

Năm	2017	2018	2019	2020
Tổng thu nhập (tỷ đồng)	?	?	?	?

b) Căn cứ vào số liệu thống kê trên một bài báo đã nêu ra nhận định : “Tổng thu nhập của người lao động Việt nam trong sản xuất thiết bị điện năm 2017 so với năm 2019 giảm xấp xỉ 20,6%”. Em hãy cho biết nhận định của bài báo có chính xác không?

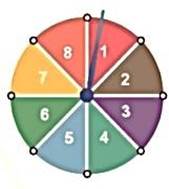
2) Hình bên mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số 1; 2; 3; 4; 5; 6; 7; 8. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần. Tính xác suất của các biến cố sau: a) “Mũi tên chỉ vào hình quạt ghi số nhỏ hơn 4”. b) “Mũi tên chỉ vào hình quạt ghi số nguyên tố”.

Gọi giá niêm yết của một chiếc ti vi khi là \[x\] (triệu đồng) .

Giá niêm yết của một chiếc máy giặt là \[y\] (triệu đồng) \[\left( {0 < x,\,\,y < 28,5} \right).\]

Giá niêm yết một tivi và một máy giặt có tổng số tiền là \[28,5\] triệu đồng nên ta có phương trình:

\[x + y = 28,5.\] (1)

Sau khi giảm \[20\% \], giá của một chiếc ti vi là \[\left( {100\% - 20\% } \right)x = 0,8x\] (triệu đồng).

Khi giảm 25% ,giá của một chiếc máy giặt là: \[\left( {100\% - 25\% } \right)y = 0,75y\] (triệu đồng)

Theo bài ra ta có phương trình: \[0,8x\; + 0,75y\; = 22.\]      (2)

Từ (1) và (2) ta có hệ phương trình \[\left\{ \begin{array}{l}x + y = 28,5\\0,8x\; + 0,75y\; = 22\end{array} \right.\].

Giải hệ phương trình trên, ta được \[\left\{ \begin{array}{l}x = 12,5\\y\; = 16\end{array} \right.\] (TMĐK).

Vậy giá niêm yết của một chiếc ti vi và máy giặt lần lượt là \[12,5\] triệu đồng và 16 triệu đồng.

1) a) Ta có \(C = \sin 30^\circ - \frac{{\tan 29^\circ }}{{\cot 61^\circ }} - 2{\cos ^2}60^\circ + \cot 45^\circ \)

\( = \frac{1}{2} - \frac{{\tan 29^\circ }}{{\tan 29^\circ }} - 2{\left( {\frac{1}{2}} \right)^2} + 1\)

\( = \frac{1}{2} - 1 - 2 \cdot \frac{1}{4} + 1 = 0.\)

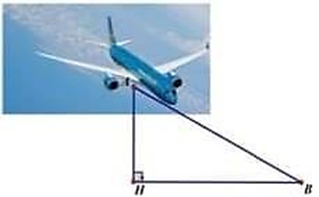
b) Xét \[\Delta ABH\] vuông tại \[H\] có: \(\sin B = \frac{{AH}}{{AB}} = \frac{{3,2}}{{6,8}} = \frac{8}{{17}}.\)

Suy ra \[\widehat B \approx 28^\circ .\]

2)

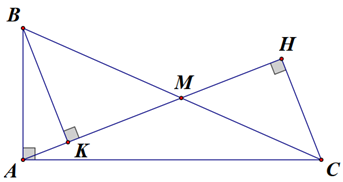
a) Vì tam giác \[ABC\] vuông tại \[A\] nên \(\widehat {BAC} = 90^\circ \); \(\widehat {ABC} + \widehat {ACB} = 90^\circ \).

Ta có \(\widehat {ABC} + \widehat {ACB} = 90^\circ \) nên \(\widehat {ACB} = 90^\circ - \widehat {ABC} = 90^\circ - 53^\circ = 37^\circ .\)

Xét tam giác \[ABC\] vuông tại \[A\] có

• \(AC = AB \cdot \tan B = 6\tan 53^\circ \approx 8\,\,({\rm{cm}}).\)

• \(AC = BC \cdot \sin B\) suy ra \[BC = \frac{{AC}}{{\sin B}} = \frac{8}{{\sin 53^\circ }} \approx 10\,\,({\rm{cm}}).\]

b) Xét \[\Delta ABK\] và \[\Delta CAH\] có

\[\widehat {ABK} = \widehat {CAH}\] (cùng phụ \(\widehat {BAH}\,).\)

\[\widehat {AKB} = \widehat {AHC} = 90^\circ \]

Do đó  (g.g).

Suy ra \[\frac{{BK}}{{AH}} = \frac{{AB}}{{AC}}\]

Do đó \[BK = AH \cdot \frac{{AB}}{{AC}} = AH \cdot \cot \widehat {ABC}\].

c) Ta có \(\frac{{MB}}{{MC}} = \frac{{BK}}{{CH}} = \frac{{AH \cdot \cot \widehat {ABC}}}{{CH}} = \frac{{AH \cdot \cot \widehat {ACB}}}{{CH}}.\)

Vì  nên \(\frac{{KA}}{{HC}} = \frac{{AB}}{{AC}},\) suy ra \[\frac{1}{{HC}} = \frac{{AB}}{{AC}}:KA = \frac{{\tan ACB}}{{KA}}\].

Do đó \[\frac{{MB}}{{MC}} = \frac{{AH \cdot {{\tan }^2}\widehat {ACB}}}{{AK}}.\]