Trong phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian Oxyz, một drone giao hàng đang ở tọa độ A(1; 0; 1) di chuyển đến địa điểm nhận hàng là B(4; 4; 6). Mỗi đơn vị trên phần mềm bằng 1 km ngoài thực tế. Biết tốc độ của drone là 80 km/h. Giả sử rằng từ vị trí giao hàng và nhận hàng không gặp chướng ngại vật, sức cản gió khống đáng kể để drone bay theo đường thẳng. Thời gian drone bay từ vị trí ban đến đến địa điểm giao hàng mất bao nhiêu phút (làm tròn đến hàng phần mười).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có \(AB = \sqrt {{{\left( {4 - 1} \right)}^2} + {{\left( {4 - 0} \right)}^2} + {{\left( {6 - 1} \right)}^2}} = 5\sqrt 2 \) (đơn vị trên phần mềm) khoảng cách ngoài thực tế sẽ là \(5\sqrt 2 \) km.
Thời gian bay của drone là \(\frac{{5\sqrt 2 }}{{80}}\) giờ ≈ 5,3 phút.
Trả lời: 5,3.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có MA2 + MB2 = (1 – a)2 + (2 – b)2 + 12 + (2 – a)2 + (−1 – b)2 + 32
= 2a2 – 6a + 2b2 – 2b + 20 = \(2{\left( {a - \frac{3}{2}} \right)^2} + 2{\left( {b - \frac{1}{2}} \right)^2} + 15 \ge 15\).
Đẳng thức xảy ra khi \(a = \frac{3}{2};b = \frac{1}{2}\). Khi đó a + b = 2.
Trả lời: 2.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
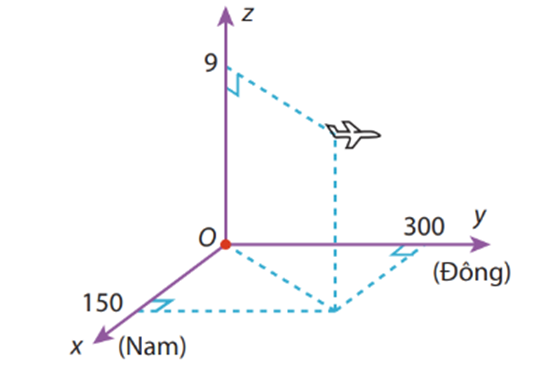
. a) Dựa vào hình vẽ ta thấy máy bay đang ở độ cao 9 km.
b) Máy bay ở tọa độ (150; 300;9).
c) Vận tốc gió 10 m/s = 36 km/h.
Quãng đường máy bay bay được là 750 + 36 = 786 km.
Do đó tọa độ của máy bay là (150; 1086; 9).
d) Quãng đường máy bay bay được là \(800.\frac{1}{2} = 400\) km. Do đó tọa độ máy bay là (150; 686; 9).
Đáp án: a) Đúng; b) Sai; c) Đúng; d) Sai.
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\overrightarrow u = \left( { - 7;7; - 8} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập