khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 12
  3. Toán

Câu hỏi:

25/08/2025 937 Lưu

PHẦN II. TỰ LUẬN

Một nhà sản xuất cần làm những hộp đựng hình trụ có thể tích \[330{\rm{ml}}.\] Tìm bán kính của hộp đựng để chi phí vật liệu dùng để sản xuất là nhỏ nhất (đơn vị: cm).

Xem lời giải

Câu hỏi trong đề: Bộ 5 đề thi giữa kì 1 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Lời giải

Giả sử chi phí sản suất các mặt hình trụ là như nhau và các mép nối không đáng kể.

Ta có, thể tích hình trụ là \(V = \pi {r^2}h = 330{\rm{ (ml)}} = 330{\rm{ (c}}{{\rm{m}}^3}) \Rightarrow h = \frac{{330}}{{\pi {r^2}}}{\rm{ (cm)}}{\rm{.}}\)

Diện tích toàn phần của hộp đựng là: \(S\left( r \right) = 2\pi {r^2} + 2\pi r \cdot h = 2\pi {r^2} + \frac{{660}}{r}\).

Ta có \(S'\left( r \right) = 4\pi r - \frac{{660}}{{{r^2}}};\,\,S'\left( r \right) = 0 \Rightarrow {r^3} = \frac{{165}}{\pi } \Rightarrow r = \sqrt[3]{{\frac{{165}}{\pi }}}{\rm{ (cm)}}\).

Bảng biến thiên

Một nhà sản xuất cần làm những hộp đựng hình trụ có thể tích \[330{\rm{ml}}.\] Tìm bán kính của hộp đựng để chi phí vật liệu dùng để sản xuất là nhỏ nhất (đơn vị: cm). (ảnh 1)

Từ bảng biến thiên, ta kết luận \(r = \sqrt[3]{{\frac{{165}}{\pi }}}{\rm{ (cm)}}\) thì chi phí vật liệu dùng để sản xuất là nhỏ nhất.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Đường cong cho trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây?

Đường cong cho trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây? (ảnh 1)
A. \[y = \frac{{{x^2} - 2x + 2}}{{x + 1}}\].   
B. \[y = \frac{{{x^2} + x + 1}}{{ - x + 1}}\]. 
C. \[y = \frac{{{x^2} - x + 1}}{{ - x + 1}}\].      
D. \[y = \frac{{ - {x^2} - x - 1}}{{2x - 1}}\].

Lời giải

Lời giải

Đồ thị hàm số có tiệm cận đứng \(x = 1\) nên loại A, D.

Đồ thị hàm số có tiệm cận xiên \(y =  - x\) nên loại B. Chọn C.

Câu 2

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, \(SA = SB = AB\). Gọi \(\alpha \) là góc giữa hai vectơ \(\overrightarrow {CD} \) và \(\overrightarrow {AS} \). Tính \(\cos \alpha \).

A. \[ - \frac{1}{2}\].             

B. \[\frac{1}{2}\].             
C. \[\frac{{\sqrt 3 }}{2}\].            
D. \[ - \frac{{\sqrt 3 }}{2}\].

Lời giải

Lời giải

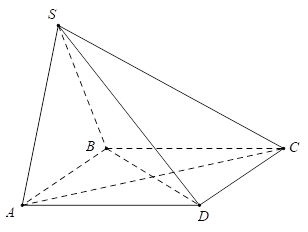
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, \(SA = SB = AB\). Gọi \(\alpha \) là góc giữa hai vectơ \(\overrightarrow {CD} \) và \(\overrightarrow {AS} \). Tính \(\cos \alpha \). (ảnh 1)

Vì \[SA = SB = AB\] nên tam giác \[SAB\] đều, do đó \[\left( {\overrightarrow {AB} ,\overrightarrow {AS} } \right) = 60^\circ \].

Ta có \[\alpha  = \left( {\overrightarrow {CD} ,\overrightarrow {AS} } \right) = \left( {\overrightarrow {BA} ,\overrightarrow {AS} } \right) = 180^\circ  - \left( {\overrightarrow {AB} ,\overrightarrow {AS} } \right)\]\[ = 180^\circ  - 60^\circ  = 120^\circ \].

Suy ra \[\cos \alpha  = \frac{{ - 1}}{2}\]. Chọn A.

Câu 3

Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x\left( {x - 1} \right){\left( {x - 2} \right)^2}\left( {{x^2} - 1} \right)\), \(\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là

A. \(0\).  

B. \[3\].  
C. \(1\). 
D. \(2\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Chi phí nhiên liệu của một chiếc tàu chạy trên sông được chia làm hai phần. Phần thứ nhất không phụ thuộc vào vận tốc và bằng 480 nghìn đồng trên 1 giờ. Phần thứ hai tỉ lệ thuận với bình phương của vận tốc, khi \(v = 10\) (km/giờ) thì phần thứ hai bằng 10 nghìn đồng/giờ. Biết tàu chạy với vận tốc \(v = 30\) (km/giờ), tổng chi phí nhiên liệu trên 1 km đường sông là bao nhiêu nghìn đồng?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một chất điểm ở vị trí đỉnh \(A\) của hình lập phương \(ABCD.A'B'C'D'\). Chất điểm chịu tác động bởi ba lực \(\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c \) lần lượt cùng hướng với \(\overrightarrow {AD} ,\,\overrightarrow {AB} ,\,\overrightarrow {AC'} \) như hình vẽ.

Tính độ lớn hợp lực của các lực \(\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c \). (ảnh 1)

Độ lớn của các lực \(\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c \) tương ứng là 10 N, 10 N và 20 N. Tính độ lớn hợp lực của các lực \(\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c \).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

B. TRẮC NGHIỆM ĐÚNG - SAI.  Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) \(\left( {a \ne 0} \right)\) và có đồ thị là đường cong như hình.

a) Hệ số \[a < 0\]. b) Đồ thị hàm số \(y = f\left( x \right)\) có điểm cực tiểu là \(\left( {1;\,3} \right)\). c) Hàm số đồng biến trên khoảng \(\left( { - 1;\,1} \right)\). d) \[f\left( 3 \right) =  - 5\]. (ảnh 1)

a) Hệ số \[a < 0\].

b) Đồ thị hàm số \(y = f\left( x \right)\) có điểm cực tiểu là \(\left( {1;\,3} \right)\).

c) Hàm số đồng biến trên khoảng \(\left( { - 1;\,1} \right)\).

d) \[f\left( 3 \right) =  - 5\].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập