C. TRẢ LỜI NGẮN.
Trong một thí nghiệm y học, người ta cấy \(900\) con vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo giời gian bởi công thức: \(N\left( t \right) = 900 + \frac{{100t}}{{100 + {t^2}}}\) (con), trong đó \(t\) là thời gian tính bằng giây \(\left( {t \ge 0} \right)\). Trong khoảng thời gian \(\left( {a;b} \right)\) từ lúc nuôi cấy thì số lượng vi khuẩn sẽ tăng lên. Tính \(3a + \,2b\).
C. TRẢ LỜI NGẮN.
Trong một thí nghiệm y học, người ta cấy \(900\) con vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo giời gian bởi công thức: \(N\left( t \right) = 900 + \frac{{100t}}{{100 + {t^2}}}\) (con), trong đó \(t\) là thời gian tính bằng giây \(\left( {t \ge 0} \right)\). Trong khoảng thời gian \(\left( {a;b} \right)\) từ lúc nuôi cấy thì số lượng vi khuẩn sẽ tăng lên. Tính \(3a + \,2b\).
Quảng cáo
Trả lời:
Lời giải
Ta có \(N'\left( t \right) = \frac{{100\left( {100 + {t^2}} \right) - 100t \cdot 2t}}{{{{\left( {100 + {t^2}} \right)}^2}}} = \frac{{100\left( {100 - {t^2}} \right)}}{{{{\left( {100 + {t^2}} \right)}^2}}}\).
\(N'\left( t \right) = 0\) khi \(t = 10\).
Bảng biến thiên:
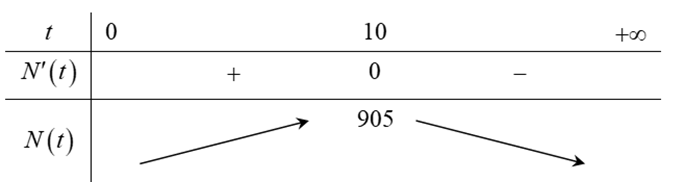
Từ bảng biến thiên, ta thấy trong khoảng thời gian \(\left( {0;\,10} \right)\) từ lúc nuôi cấy thì số lượng vi khuẩn sẽ tăng lên.
Khi đó, ta có: \(a = 0,\,\,b = 10\). Vậy \(3a\, + \,2b = 20\).
Đáp án: 20.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
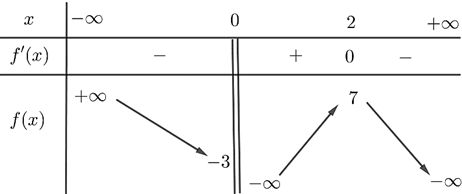
A. \(y = \frac{{ - x + 2}}{{x - 1}}\).
Lời giải
Lời giải
Dựa vào bảng biến thiên ta có đồ thị hàm số có đường tiệm cận đứng là \(x = 1\) và đường tiệm cận ngang là \(y = 1\). Suy ra loại A, C.
Xét câu B, \(y' = \frac{{ - 3}}{{{{\left( {x - 1} \right)}^2}}} < 0,\,\forall x \ne 1\).
Xét câu D, \(y' = \frac{2}{{{{\left( {x - 1} \right)}^2}}} > 0,\,\forall x \ne 1\).
Chọn B.
Câu 2
Lời giải
Lời giải
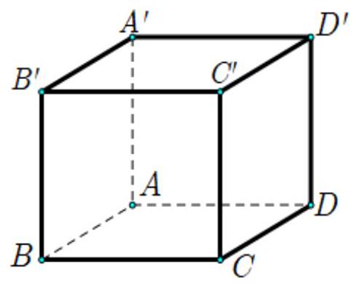
Ta có \(\vec u = \overrightarrow {A'C'} - \overrightarrow {A'A} = \overrightarrow {AC'} \).
Suy ra \(\left| {\vec u} \right| = \left| {\overrightarrow {AC'} } \right| = AC' = \sqrt {A{{A'}^2} + A{B^2} + A{D^2}} = \sqrt {{2^2} + {2^2} + {2^2}} = 2\sqrt 3 \). Chọn D.
Câu 3
A. \(y = - 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
B. TRẮC NGHIỆM ĐÚNG - SAI. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\).
a) Hàm số đã cho đồng biến trên \[\left( { - \infty ; - 1} \right)\] và \(\left( {3; + \infty } \right)\).
b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng \( - 4\).
c) Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm \(A\left( {0;1} \right)\).
d) Phương trình tiếp tuyến của đồ thị hàm số đã cho vuông góc với đường thẳng \(x - 3y - 6 = 0\) đi qua điểm \(B\left( { - \frac{3}{2};\frac{3}{2}} \right)\).
B. TRẮC NGHIỆM ĐÚNG - SAI. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\).
a) Hàm số đã cho đồng biến trên \[\left( { - \infty ; - 1} \right)\] và \(\left( {3; + \infty } \right)\).
b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng \( - 4\).
c) Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm \(A\left( {0;1} \right)\).
d) Phương trình tiếp tuyến của đồ thị hàm số đã cho vuông góc với đường thẳng \(x - 3y - 6 = 0\) đi qua điểm \(B\left( { - \frac{3}{2};\frac{3}{2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
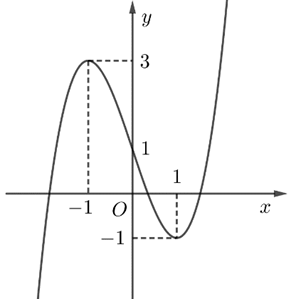
A. \(\left( { - 1;\;3} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số \[y = f\left( x \right)\] xác định trên \[\mathbb{R}\backslash \left\{ 1 \right\}\], liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau: Bảng biến thiên trên của hàm số nào trong các hàm số sau? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/08/blobid10-1756171849.png)