Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị \(\left( C \right)\). Biết \(y = f'\left( x \right)\) có đồ thị như hình vẽ và tâm đối xứng của đồ thị \(\left( C \right)\) thuộc trục hoành. Tính khoảng cách giữa hai điểm cực trị của đồ thị \(\left( C \right)\). (Quy tròn kết quả đến hàng phần trăm).
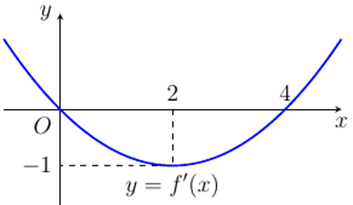
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị \(\left( C \right)\). Biết \(y = f'\left( x \right)\) có đồ thị như hình vẽ và tâm đối xứng của đồ thị \(\left( C \right)\) thuộc trục hoành. Tính khoảng cách giữa hai điểm cực trị của đồ thị \(\left( C \right)\). (Quy tròn kết quả đến hàng phần trăm).

Quảng cáo
Trả lời:
Lời giải
Parabol \(y' = f'\left( x \right) = 3a{x^2} + 2bx + c\) có đỉnh \(\left( {2;\,\, - 1} \right)\) và đi qua \(O\left( {0;\,\,0} \right)\) nên ta có hệ phương trình
\[\left\{ {\begin{array}{*{20}{c}}{ - \frac{{2b}}{{6a}} = 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\\begin{array}{l}12a + 4b + c = - 1\\c = 0\end{array}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}\begin{array}{l}a = \frac{1}{{12}}\\b = - \frac{1}{2}\end{array}\\{c = 0\,\,\,\,\,}\end{array}} \right.\].
Tâm đối xứng của \(\left( C \right)\) thuộc trục hoành nên suy ra tâm đối xứng có toạ độ \(\left( {2;\,\,0} \right)\).
Do đó \(\frac{{{2^3}}}{{12}} - \frac{{{2^2}}}{2} + d = 0 \Leftrightarrow d = \frac{4}{3}\).
Khi đó, đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^3}}}{{12}} - \frac{{{x^2}}}{2} + \frac{4}{3}\) có hai điểm cực trị là \(A\left( {0;\,\,\frac{4}{3}} \right)\) và \(B\left( {4;\,\, - \frac{4}{3}} \right)\).
Vậy \(AB = \sqrt {{4^2} + {{\left( { - \frac{8}{3}} \right)}^2}} = \frac{{4\sqrt {13} }}{3} \approx 4,81\).
Đáp án: 4,81.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Lời giải
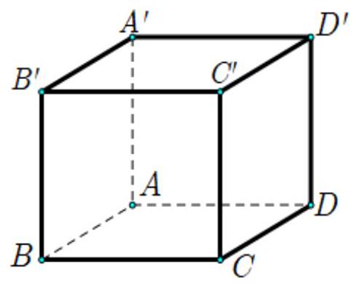
Ta có \(\vec u = \overrightarrow {A'C'} - \overrightarrow {A'A} = \overrightarrow {AC'} \).
Suy ra \(\left| {\vec u} \right| = \left| {\overrightarrow {AC'} } \right| = AC' = \sqrt {A{{A'}^2} + A{B^2} + A{D^2}} = \sqrt {{2^2} + {2^2} + {2^2}} = 2\sqrt 3 \). Chọn D.
Câu 2
A. \(y = \frac{{ - x + 2}}{{x - 1}}\).
Lời giải
Lời giải
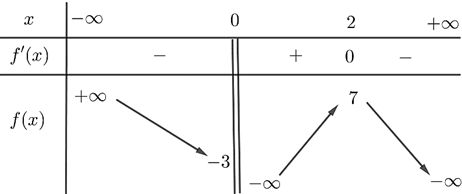
Dựa vào bảng biến thiên ta có đồ thị hàm số có đường tiệm cận đứng là \(x = 1\) và đường tiệm cận ngang là \(y = 1\). Suy ra loại A, C.
Xét câu B, \(y' = \frac{{ - 3}}{{{{\left( {x - 1} \right)}^2}}} < 0,\,\forall x \ne 1\).
Xét câu D, \(y' = \frac{2}{{{{\left( {x - 1} \right)}^2}}} > 0,\,\forall x \ne 1\).
Chọn B.
Câu 3
A. \(y = - 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
B. TRẮC NGHIỆM ĐÚNG - SAI. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\).
a) Hàm số đã cho đồng biến trên \[\left( { - \infty ; - 1} \right)\] và \(\left( {3; + \infty } \right)\).
b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng \( - 4\).
c) Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm \(A\left( {0;1} \right)\).
d) Phương trình tiếp tuyến của đồ thị hàm số đã cho vuông góc với đường thẳng \(x - 3y - 6 = 0\) đi qua điểm \(B\left( { - \frac{3}{2};\frac{3}{2}} \right)\).
B. TRẮC NGHIỆM ĐÚNG - SAI. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\).
a) Hàm số đã cho đồng biến trên \[\left( { - \infty ; - 1} \right)\] và \(\left( {3; + \infty } \right)\).
b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng \( - 4\).
c) Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm \(A\left( {0;1} \right)\).
d) Phương trình tiếp tuyến của đồ thị hàm số đã cho vuông góc với đường thẳng \(x - 3y - 6 = 0\) đi qua điểm \(B\left( { - \frac{3}{2};\frac{3}{2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\left( { - 1;\;3} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số \[y = f\left( x \right)\] xác định trên \[\mathbb{R}\backslash \left\{ 1 \right\}\], liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau: Bảng biến thiên trên của hàm số nào trong các hàm số sau? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/08/blobid10-1756171849.png)