Trong không gian \[{\rm{Ox}}yz\], cho điểm \[D\left( {4; - 1;3} \right)\] và các điểm \[M,N,P\] lần lượt thuộc các trục \[{\rm{Ox}},\,Oy,Oz\] sao cho \[DM,DN,DP\] đôi một vuông góc với nhau
a) Tung độ của điểm \[N\] bằng \[13\].
b) Cao độ của điểm \[P\] bằng \[\frac{{13}}{4}\].
c) \[{V_{DMNP}} > 29\].
d) Gọi \[\overrightarrow x \] là vectơ thỏa \[\overrightarrow x .\overrightarrow {DM} = 1;\,\,\overrightarrow x .\overrightarrow {DN} = 2;\,\,\overrightarrow x .\overrightarrow {DP} = - 3\] thì tổng hoành độ, tung độ và cao độ của vectơ \[\overrightarrow x \] thuộc khoảng \[\left( {3;7} \right)\].
Quảng cáo
Trả lời:
Gọi \[M\left( {a\,;0\,;0} \right),N\left( {0\,;b\,;0} \right),P\left( {0\,;0\,;\,c} \right)\].
\[\begin{array}{l}\overrightarrow {DM} = \left( {a - 4;1; - 3} \right)\\\overrightarrow {DN} = \left( { - 4;b + 1; - 3} \right)\\\overrightarrow {DP} = \left( { - 4;1;c - 3} \right)\end{array}\]
Ta có \[DM,DN,DP\] đôi một vuông góc với nhau nên
\[\left\{ \begin{array}{l}\overrightarrow {DM} .\overrightarrow {DN} = 0\\\overrightarrow {DM} .\overrightarrow {DP} = 0\\\overrightarrow {DN} .\overrightarrow {DP} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 4\left( {a - 4} \right) + b + 1 + 9 = 0\\ - 4\left( {a - 4} \right) + 1 - 3\left( {c - 3} \right) = 0\\16 + b + 1 - 3\left( {c - 3} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 4a + b = - 26\\ - 4a - 3c = - 26\\b - 3c = - 26\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{13}}{4}\\b = - 13\\c = \frac{{13}}{3}\end{array} \right.\].
a) Sai.
b) Sai.
c) Đúng vì: \[{V_{DMNP}} = \frac{1}{6}DM.DN.DP = \frac{1}{6}.\frac{{13}}{4}.13.\frac{{13}}{3} = \frac{{2197}}{{72}} > 29\].
d) Gọi \[\overrightarrow x = \left( {m\,;n\,;p} \right)\]
\[\overrightarrow {DM} = \left( { - \frac{3}{4};\,1\,; - 3} \right);\,\,\overrightarrow {DN} = \left( { - 4; - 12; - 3} \right);\,\,\,\overrightarrow {DP} = \left( { - 4;1\,;\,\frac{4}{3}} \right)\]
\[\left\{ \begin{array}{l}\overrightarrow x .\overrightarrow {DM} = 1\\\overrightarrow x .\overrightarrow {DN} = 2\\\overrightarrow x .\overrightarrow {DP} = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - \frac{3}{4}m + n - 3p = 1\\ - 4m - 12n - 3p = 2\\ - 4m + n + \frac{4}{3}p = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = \frac{{88}}{{169}}\\n = - \frac{{35}}{{169}}\\p = - \frac{{90}}{{169}}\end{array} \right.\]
\[m\, + n\, + p = \frac{{ - 37}}{{169}}\].
Suy ra d) sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời : \(1,15\)
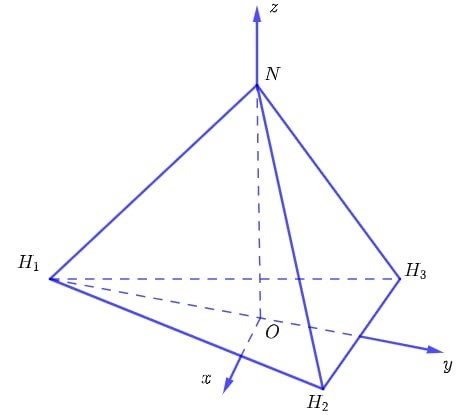
Gọi \(a = {H_1}{H_2}\) là khoảng cách giữa hai nguyên tử hydrogen , khi đó độ dài \(O{H_1} = \frac{{\sqrt 3 }}{2}{H_1}{H_2} \Leftrightarrow \sqrt 3 = \frac{{\sqrt 3 a}}{2} \Rightarrow a = 2\).
Giả sử góc tạo bởi liên kết \(H - N - H,\) có hai cạnh là hai đoạn thẳng nối \(N\) với hai trong ba điểm \({H_1},\,{H_2},\,{H_3}\) là góc \(\widehat {{H_2}N{H_3}} = {120^ \circ }\)
Gọi \(x\) là khoảng cách giữa nguyên tử nitrogen với mỗi nguyên tử hydrogen, khi đó \(N{H_2} = x\)
Áp dụng định lý cosin ta có:
\({H_2}{H_3} = N{H_2}^2 + N{H_3}^2 - 2.N{H_2}.N{H_3}.\cos \widehat {{H_2}N{H_3}}\)\( \Leftrightarrow 4 = {x^2} + {x^2} - 2{x^2}\cos {120^ \circ } \Rightarrow {x^2} = \frac{4}{3} \Rightarrow x = \frac{{2\sqrt 3 }}{3} \approx 1,15 \cdot \)
Lời giải
a) Đúng.
Ta có \[\overrightarrow x = \overrightarrow a + \overrightarrow b = (3;4;2)\] .
b) Sai.
Ta có \[\overrightarrow y = \overrightarrow a + \overrightarrow c = (5;2; - 1)\].
c) Sai.
Ta có \[\overrightarrow z = \overrightarrow b + \overrightarrow c = (6;2; - 5)\].
d) Đúng.
Ta có \(\overrightarrow k = \overrightarrow a + \overrightarrow b + \overrightarrow c = (7;4; - 2)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.