Một chiếc đèn trang trí hình tròn được treo song song với mặt phẳng trần nhà nằm ngang bởi ba sợi dây không giãn \(OA,\,OB,\,OC\) đôi một vuông góc (như hình vẽ dưới đây). Biết lực căng dây tương ứng trên mỗi dây \(OA,\,OB,\,OC\) lần lượt là \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} ,\,\overrightarrow {{F_3}} \) thỏa mãn \[\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right| = 16\](N). Tính trọng lượng (đơn vị: N) của chiếc đèn đó. (Làm tròn kết quả đến hàng phần chục).
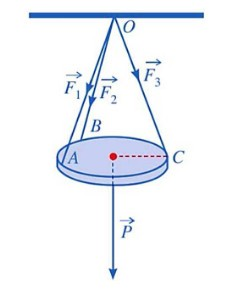
Một chiếc đèn trang trí hình tròn được treo song song với mặt phẳng trần nhà nằm ngang bởi ba sợi dây không giãn \(OA,\,OB,\,OC\) đôi một vuông góc (như hình vẽ dưới đây). Biết lực căng dây tương ứng trên mỗi dây \(OA,\,OB,\,OC\) lần lượt là \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} ,\,\overrightarrow {{F_3}} \) thỏa mãn \[\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right| = 16\](N). Tính trọng lượng (đơn vị: N) của chiếc đèn đó. (Làm tròn kết quả đến hàng phần chục).
Câu hỏi trong đề: Đề kiểm tra Ôn tập cuối chương 2 (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
ĐS: \(27,7\)
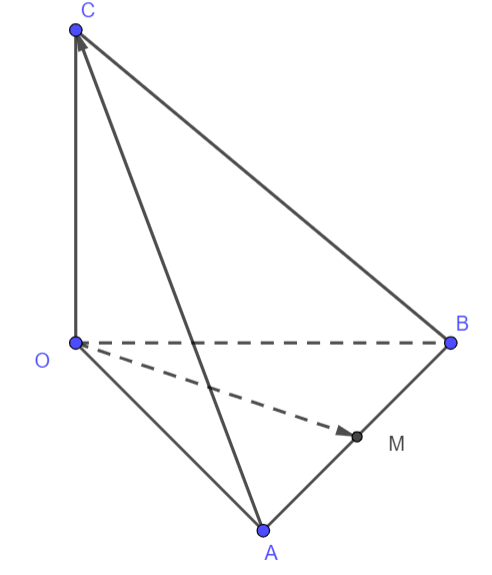
Ta có: \[P = \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right|\].
Vẽ hình vuông \(OAEB\), ta có \[\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OE} \]. (Quy tắc hình bình hành)
Vẽ hình chữ nhật \(OCFE\), ta có \[\overrightarrow {OC} + \overrightarrow {OE} = \overrightarrow {OF} \]. (Quy tắc hình bình hành)
Suy ra: \[P = \left| {\overrightarrow {OF} } \right| = OF\].
Xét hình vuông \(OAEB\), cạnh \(16\), có đường chéo \(OE = 16\sqrt 2 \).
Xét tam giác vuông \(OEF\), vuông tại \(E\), có \(OF = \sqrt {O{E^2} + E{F^2}} = \sqrt {{{\left( {16\sqrt 2 } \right)}^2} + {{16}^2}} = 16\sqrt 3 \approx 27,7\)
Vậy \(P \approx 27,7\)(N).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
ĐS: \(3,74\).
Ta có: \[{\left| {\vec a + \vec b} \right|^2} = {\left( {\vec a + \vec b} \right)^2} = {\left| {\vec a} \right|^2} + 2\vec a\vec b + {\left| {\vec b} \right|^2}\]\( \Rightarrow 2\vec a\vec b = {\left| {\vec a + \vec b} \right|^2} - {\left| {\vec a} \right|^2} - {\left| {\vec b} \right|^2} = 11\).
\[{\left| {\vec a - \vec b} \right|^2} = {\left( {\vec a - \vec b} \right)^2} = {\left| {\vec a} \right|^2} - 2\vec a\vec b + {\left| {\vec b} \right|^2} = 9 - 11 + 16 = 14\]\( \Rightarrow \left| {\vec a - \vec b} \right| = \sqrt {14} \approx 3,74\).
Lời giải
a) Đ
b) S
c) Đ
Gọi \(D\left( {x;\,\,y} \right)\). Khi đó , \(\overrightarrow {DC} = \left( {1 - x;\,\,1 - y;\, - 2 - z\,} \right)\)
Vì \(ABCD\)là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \Rightarrow \left\{ \begin{array}{l} - 3 = 1 - x\\ - 1 = 1 - y\\ - 1 = - 2 - z\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 4\\y = 2\\z = - 1\end{array} \right.\)
Vậy \(D\left( {4;\,\,2;\,\, - 1} \right)\)
d) Đ
Gọi \(H\left( {x;y;z} \right)\) là trực tâm tam giác \(ABC\).
Khi đó tọa độ điểm \(H\) thỏa mãn \( \Leftrightarrow \)\(\left\{ \begin{array}{l}\overrightarrow {AH} .\overrightarrow {BC} = 0\\\overrightarrow {BH} .\overrightarrow {AC} = 0\\\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AH} \, = 0\end{array} \right.\)\( \Leftrightarrow \)\(\left\{ \begin{array}{l}2x - y - 2z = - 1\\x + 2y + 3z = 3\\x - 8y + 5z = - 17\end{array} \right.\).
Suy ra \(H\left( {\frac{2}{{15}};\frac{{29}}{{15}}; - \frac{1}{3}} \right)\).
Vậy \[OH = \frac{{\sqrt {870} }}{{15}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(M\left( { - 4;0;0} \right).\)
B. \(M\left( {5;0;0} \right).\)
C. \(M\left( {4;0;0} \right).\)
D. \(M\left( { - 5;0;0} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập