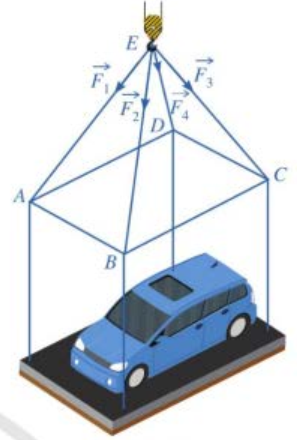
Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật ABCD, mặt phẳng (ABCD) song song với mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc E của chiếc cần cẩu sao cho các đoạn dây cáp EA, EB, EC, ED có độ dài bằng nhau và cùng tạo với mặt phẳng (ABCD) một góc bằng ${45^0}$. Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Biết trọng lượng chiếc xe ô tô là \[4000\,N\] và trọng lượng khung sắt là \[2000N\]; cường độ các lực căng $\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\,\overrightarrow {{F_3}} ,\,\overrightarrow {{F_4}} $ là bằng nhau. Tính cường độ lực căng $\overrightarrow {{F_1}} $

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra Ôn tập cuối chương 2 (có lời giải) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

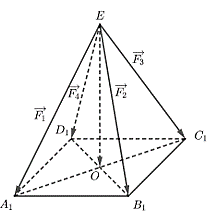
Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật ABCD, mặt phẳng (ABCD) song song với mặt phẳng nằm ngang. (ảnh 2)

Ta đơn giản hoá mô hình bài toán thông qua hình vẽ sau ($\overrightarrow {EO} $ cùng hướng với véctơ trọng lực của ô tô và khung sắt).

Theo giả thiết ta có $\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} , + \overrightarrow {{F_3}} + \,\overrightarrow {{F_4}} } \right| = 6000.$Mặt khác:$\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + \,\overrightarrow {{F_4}} } \right| = \left| {4\overrightarrow {EO} } \right| = 4EO.$

Suy ra $EO = 1500.$

Ta có $\left( {ED,(ABCD)} \right) = \widehat {EDO} = {45^0}$. Như vậy $ED = \frac{{EO}}{{\sin {{45}^0}}} = 1500\sqrt 2 .$

Cường độ lực căng $\overrightarrow {{F_1}} $ là $1500\sqrt 2 N$.

Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

PHẦN 2. CÂU HỎI DẠNG ĐÚNG – SAI (4 CÂU)

Cho hình lăng trụ tam giác đều ABC.A'B'C' có \[AB = a\] và \[AA' = a\sqrt 2 \]. Các mệnh đề dưới đây đúng hay sai?

a) $\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} $

b) Gọi \[M\] là trung điểm $BC$ khi đó $\overrightarrow {A'M} = \overrightarrow {A'A} + \overrightarrow {A'B'} - \overrightarrow {CM} $.

c) $\overrightarrow {A'M} .\overrightarrow {AC} = \frac{{{a^2}\sqrt 3 }}{4}$.

d) Góc giữa vectơ \[\overrightarrow {AB'} \] và $\overrightarrow {BC'} $ bằng $60^\circ $.

Xem đáp án

Lời giải

$Cho hình lăng trụ tam giác đều ABC.A'B'C' có \[AB = a\] và \[AA' = a\sqrt 2 \]. Các mệnh đề dưới đây đúng hay sai? (ảnh 1)$

a) Đúng.

b) Đúng.

Ta có: $\overrightarrow {A'A} + \overrightarrow {A'B'} - \overrightarrow {CM} = \overrightarrow {A'A} + \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {A'B} + \overrightarrow {BM} = \overrightarrow {A'M} $

c) Sai.

Ta có: $\overrightarrow {A'M} .\overrightarrow {AC} = \left( {\overrightarrow {A'A} + \overrightarrow {AM} } \right).\overrightarrow {AC} = \overrightarrow {A'A} .\overrightarrow {AC} + \overrightarrow {AM} .\overrightarrow {AC} = \overrightarrow {AM} .\overrightarrow {AC} = \frac{{a\sqrt 3 }}{2}.a.\cos 30^\circ = \frac{{3{a^2}}}{4}$

d) Đúng.

Ta có $\overrightarrow {AB'} .\overrightarrow {BC'} = \left( {\overrightarrow {AB} + \overrightarrow {BB'} } \right)\left( {\overrightarrow {BC} + \overrightarrow {CC'} } \right)$$ = \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CC'} + \overrightarrow {BB'} .\overrightarrow {BC} + \overrightarrow {BB'} .\overrightarrow {CC'} $

$ = \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CC'} + \overrightarrow {BB'} .\overrightarrow {BC} + \overrightarrow {BB'} .\overrightarrow {CC'} $$ = - \frac{{{a^2}}}{2} + 0 + 0 + 2{a^2} = \frac{{3{a^2}}}{2}$

Suy ra $\cos \left( {\overrightarrow {AB'} ,\overrightarrow {BC'} } \right) = \frac{{\overrightarrow {AB'} .\overrightarrow {BC'} }}{{\left| {\overrightarrow {AB'} } \right|.\left| {\overrightarrow {BC'} } \right|}}$$ = \frac{{\frac{{3{a^2}}}{2}}}{{a\sqrt 3 .a\sqrt 3 }} = \frac{1}{2} \Rightarrow \left( {\overrightarrow {AB'} ,\overrightarrow {BC'} } \right) = 60^\circ $

Câu 2

Cho 3 điểm $A\left( { - 1\,;\,2;\,1} \right);B\left( {2; - 2;4} \right);C\left( {0; - 4;1} \right)$.

a) Ba điểm $A,\,B,C$ không thẳng hàng.

b) Điểm $D\left( {5; - 6;7} \right)$. Khi đó 3 điểm $A,B,D$ thẳng hàng .

c) \[cos\left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = \frac{{37}}{{\sqrt {1258} }}\].

d) Cho $\overrightarrow u \left( {x - 1;2y + 1;3z - 5} \right)$ thoả mãn $\overrightarrow u \bot \overrightarrow {AB} ;\overrightarrow u \bot \overrightarrow {AC} $. Khi đó ${x^2} + {y^2} + {z^2} = 2024$

Xem đáp án

Lời giải

a) Đúng.

Ta có $\overrightarrow {AB} \left( {3;\, - 4;\,3} \right),\,\overrightarrow {AC} \left( {1; - 6;0} \right)$. Giả sử tồn tại số $k \ne 0$ sao cho $\overrightarrow {AB} = k\overrightarrow {AC} \Leftrightarrow \left\{ \begin{array}{l}3 = k\\ - 4 = - 6k\\3 = 0k\end{array} \right.$ vô nghiệm suy ra không tồn tại $k$. Suy ra 3 điểm $A,B,C$ không thẳng hàng.

b) Đúng.

Ta có $\overrightarrow {AB} \left( {3;\, - 4;\,3} \right),\,\overrightarrow {AD} \left( {6; - 8;6} \right) \Rightarrow \overrightarrow {AD} = 2\overrightarrow {AC} $. Vậy 3 điểm $A,B,D$ thẳng hàng.

c) Sai.

Ta có $cos\left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = \frac{{3 + 24}}{{\sqrt {9 + 9 + 16} .\sqrt {1 + 36} }} = \frac{{27\sqrt {1258} }}{{1258}}$.

d) Sai.

Ta có $\overrightarrow u \bot \overrightarrow {AB} ;\overrightarrow u \bot \overrightarrow {AC} \Rightarrow \overrightarrow u = \left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right] = \left( {18;3; - 14} \right) = \left( {x - 1;2x + 1;3z - 5} \right)$

Suy ra

\[\left\{ \begin{array}{l}x - 1 = 18\\2y + 1 = 3\\3z - 5 = - 14\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 19\\y = 1\\z = - 3\end{array} \right. \Rightarrow {x^2} + {y^2} + {z^2} = {19^2} + 1 + 9 = 371\]

Câu 3