B. Tự luận
Cho hình lập phươngABCD.A'B'C'D' có cạnh bằng \(5\).
a) Tìm góc giữa các cặp vectơ sau: \(\overrightarrow {AC} \) và \(\overrightarrow {AB} \); \(\overrightarrow {AC} \) và \(\overrightarrow {B'D'} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CD} \); \(\overrightarrow {AD'} \) và \(\overrightarrow {BD} \).
b) Tính các tích vô hướng:\(\overrightarrow {AC} .\overrightarrow {AB} \); \(\overrightarrow {AC} .\overrightarrow {B'D'} \); \(\overrightarrow {AD'} .\overrightarrow {BD} \).
c) Chứng minh \(\overrightarrow {AC'} \) vuông góc với \(\overrightarrow {BD} \).
B. Tự luận
Cho hình lập phươngABCD.A'B'C'D' có cạnh bằng \(5\).
a) Tìm góc giữa các cặp vectơ sau: \(\overrightarrow {AC} \) và \(\overrightarrow {AB} \); \(\overrightarrow {AC} \) và \(\overrightarrow {B'D'} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CD} \); \(\overrightarrow {AD'} \) và \(\overrightarrow {BD} \).
b) Tính các tích vô hướng:\(\overrightarrow {AC} .\overrightarrow {AB} \); \(\overrightarrow {AC} .\overrightarrow {B'D'} \); \(\overrightarrow {AD'} .\overrightarrow {BD} \).
c) Chứng minh \(\overrightarrow {AC'} \) vuông góc với \(\overrightarrow {BD} \).
Quảng cáo
Trả lời:
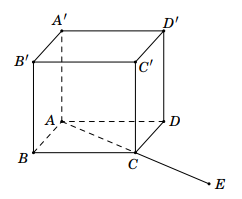
a) Ta có: \(\left( {\overrightarrow {AC} ,\overrightarrow {AB} } \right) = \widehat {CAB} = 45^\circ \); \(\left( {\overrightarrow {AC} ,\,\overrightarrow {B'D'} } \right) = \left( {\overrightarrow {AC} ,\,\overrightarrow {BD'} } \right) = 90^\circ \)
\[\left( {\overrightarrow {AC} ,\,\overrightarrow {CD} } \right) = \left( {\overrightarrow {CE} ,\,\overrightarrow {CD} } \right) = 180^\circ - 45^\circ = 135^\circ \] (\(E\) là điểm đối xứng của \(A\) qua \(C\))
\(\overrightarrow {AD'} = \overrightarrow {BC'} \Rightarrow \left( {\overrightarrow {AD'} ,\overrightarrow {BD} } \right) = \left( {\overrightarrow {BC'} ,\overrightarrow {BD} } \right) = \widehat {C'BD}\) mà tam giác \(C'BD\) là tam giác đều nên khi đó ta có \(\widehat {C'BD} = 60^\circ \).
b) Ta có \(AC = BD = B'D' = 5\sqrt 2 \) suy ra:
.
Do \(AC\) vuông góc với \(B'D'\) nên \(\overrightarrow {AC} .\overrightarrow {B'D'} = 0\).
.
c) Ta cần chứng minh \(\overrightarrow {AC'} .\overrightarrow {BD} = 0\)
Ta có: \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \) và \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} \) nên \(\overrightarrow {AC'} .\overrightarrow {BD} = \left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right).\left( {\overrightarrow {AD} - \overrightarrow {AB} } \right)\)
\[ = \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {A{B^2}} + \overrightarrow {A{D^2}} - \overrightarrow {AD} .\overrightarrow {AB} + \overrightarrow {AA'} .\overrightarrow {AD} - \overrightarrow {AA'} .\overrightarrow {AB} = {5^2} - {5^2} = 0\].
Suy ra \(\overrightarrow {AC'} \) vuông góc với \(\overrightarrow {BD} \) (điều phải chứng minh).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
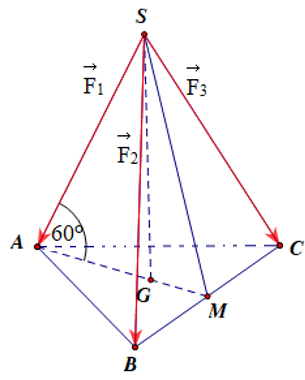
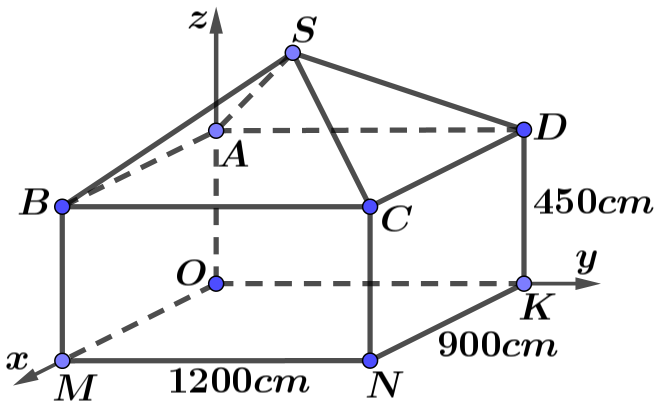
Gán các lực \[\overrightarrow {{F_1}} = \overrightarrow {SA} ,\,\,\overrightarrow {{F_2}} = \overrightarrow {SB} ,\,\,\overrightarrow {{F_3}} = \overrightarrow {SC} .\]
Vì \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right|\) và góc tạo bởi mỗi chân của giá đỡ với mặt đất bằng \(60^\circ \) nên \(S.ABC\) là hình chóp đều.
Gọi \(M\) là trung điểm \(BC,\,\,G\) là trọng tâm \(\Delta ABC \Rightarrow SG \bot \left( {ABC} \right).\)
Ta có \(\widehat {SBG} = 60^\circ \Rightarrow SG = SA.\sin 60^\circ = \frac{{SA\sqrt 3 }}{2} \Rightarrow SA = \frac{{2SG}}{{\sqrt 3 }}.\)
Đặt \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} \Rightarrow \left| {\overrightarrow F } \right| = 30\left( {\rm{N}} \right).\)
Vì \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SG} \Rightarrow \left| {\overrightarrow F } \right| = 3\left| {\overrightarrow {SG} } \right| \Rightarrow SG = \frac{{\left| {\overrightarrow F } \right|}}{3} = 10.\)
Vậy \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {SA} } \right| = 2\frac{{SG}}{{\sqrt 3 }} = \frac{{20}}{{\sqrt 3 }} \approx 11,5\left( {\rm{N}} \right).\)
Đáp án: 11,5.
Lời giải
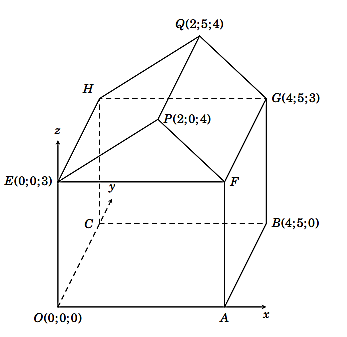
a) Sai. Vì nền nhà là hình chữ nhật nên tứ giác \(OABC\) là hình chữ nhật, suy ra \({x_A} = {x_B} = 4,{y_C} = {y_B} = \) 5. Do \(A\) nằm trên trục \(Ox\) nên tọa độ điểm \(A\) là \(\left( {4;0;0} \right)\).
b) Sai. Tường nhà là hình chữ nhật, suy ra \({y_H} = {y_C} = 5,{z_H} = {z_E} = 3\). Do \(H\) nằm trên mặt phẳng \(\left( {Oyz} \right)\) nên tọa độ điểm \(H\) là \(\left( {0;5;3} \right)\).
c) Sai. Để tính góc dốc của mái nhà, ta đi tính số đo góc nhị diện có cạnh là đường thẳng \(FG\), hai mặt phẳng lần lượt là \(\left( {FGQP} \right)\) và \(\left( {FGHE} \right)\). Do mặt phẳng \(\left( {Ozx} \right)\) vuông góc với hai mặt phẳng \(\left( {FGQP} \right)\) và \(\left( {FGHE} \right)\) nên góc \(PFE\) là góc phẳng nhị diện ứng với góc nhị diện đó.
Ta có \(\overrightarrow {FP} = \left( { - 2;0;1} \right),\overrightarrow {FE} = \left( { - 4;0;0} \right)\).
Suy ra \({\rm{cos}}\widehat {PFE} = {\rm{cos}}\left( {\overrightarrow {FP} ,\overrightarrow {FE} } \right) = \frac{{\overrightarrow {FP} \cdot \overrightarrow {FE} }}{{\left| {\overrightarrow {FP} \left| \cdot \right|\overrightarrow {FE} } \right|}} = \frac{{\left( { - 2} \right) \cdot \left( { - 4} \right) + 0 \cdot 0 + 1 \cdot 0}}{{\sqrt {{{( - 2)}^2} + {0^2} + {1^2}} \cdot \sqrt {{{( - 4)}^2} + {0^2} + {0^2}} }} = \frac{{2\sqrt 5 }}{5}\).
Do đó, \(\widehat {PFE} \approx 26,6^\circ \). Vậy góc dốc của mái nhà khoảng \(26,6^\circ \).
d) Sai. Chiều cao bằng cao độ của điểm \(P\) suy ra \(h = 4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.