Ba lực \[\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \] cùng tác dụng vào một vật có phương đôi một vuông góc với nhau và có độ lớn lần lượt là \(2\)N, \(3\)N và \(4\)N.
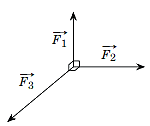
a) Tính độ lớn hợp hai lực \(\overrightarrow {{F_2}} ,\,\overrightarrow {{F_3}} \).
b) Tính độ lớn hợp lực của ba lực đã cho.
Ba lực \[\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \] cùng tác dụng vào một vật có phương đôi một vuông góc với nhau và có độ lớn lần lượt là \(2\)N, \(3\)N và \(4\)N.

a) Tính độ lớn hợp hai lực \(\overrightarrow {{F_2}} ,\,\overrightarrow {{F_3}} \).
b) Tính độ lớn hợp lực của ba lực đã cho.
Quảng cáo
Trả lời:
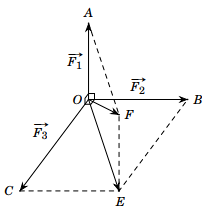
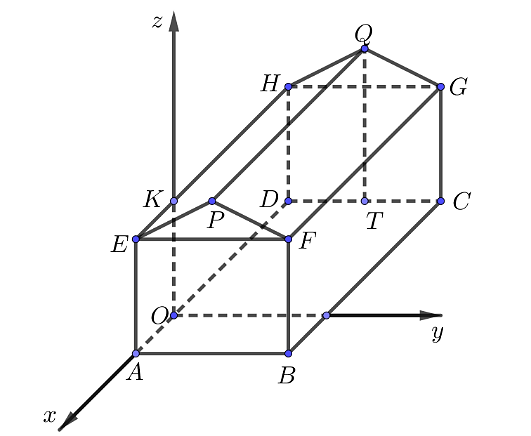
a) Gọi \(O\) là vị trí trên vật mà ba lực cùng tác động vào. Gọi \(A,\,\,B,\,\,C\) là các điểm sao cho \(\overrightarrow {{F_1}} = \overrightarrow {OA} \)\[\overrightarrow {{F_2}} = \overrightarrow {OB} \,,\,\,\overrightarrow {{F_3}} = \overrightarrow {OC} \]. Khi đó \[\left| {\overrightarrow {{F_2}} + \overrightarrow {{F_3}} } \right| = OE = \sqrt {{3^2} + {4^2}} = 5\]N.
b) Dựng các hình chữ nhật \(OBEC\) và \(OEFA\) thì ta có \(\left\{ \begin{array}{l}\overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OE} \\\overrightarrow {OA} + \overrightarrow {OE} = \overrightarrow {OF} \end{array} \right.\).
Do đó \[\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OE} = \overrightarrow {OF} \]
Vậy độ lớn hợp lực của cả ba lực là:
\(\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} } \right| = \overrightarrow {OF} = \sqrt {O{A^2} + O{E^2}} = \sqrt {O{A^2} + O{B^2} + O{C^2}} = \sqrt {{2^2} + {3^2} + {4^2}} = \sqrt {29} \)N.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
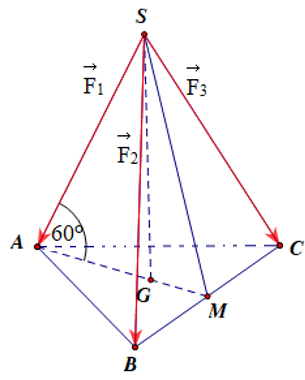
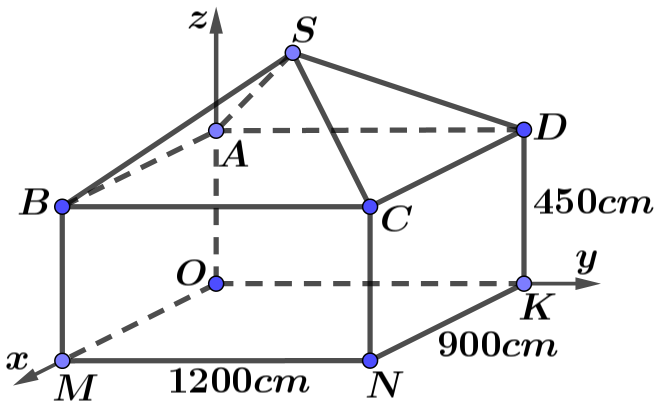
Gán các lực \[\overrightarrow {{F_1}} = \overrightarrow {SA} ,\,\,\overrightarrow {{F_2}} = \overrightarrow {SB} ,\,\,\overrightarrow {{F_3}} = \overrightarrow {SC} .\]
Vì \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right|\) và góc tạo bởi mỗi chân của giá đỡ với mặt đất bằng \(60^\circ \) nên \(S.ABC\) là hình chóp đều.
Gọi \(M\) là trung điểm \(BC,\,\,G\) là trọng tâm \(\Delta ABC \Rightarrow SG \bot \left( {ABC} \right).\)
Ta có \(\widehat {SBG} = 60^\circ \Rightarrow SG = SA.\sin 60^\circ = \frac{{SA\sqrt 3 }}{2} \Rightarrow SA = \frac{{2SG}}{{\sqrt 3 }}.\)
Đặt \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} \Rightarrow \left| {\overrightarrow F } \right| = 30\left( {\rm{N}} \right).\)
Vì \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SG} \Rightarrow \left| {\overrightarrow F } \right| = 3\left| {\overrightarrow {SG} } \right| \Rightarrow SG = \frac{{\left| {\overrightarrow F } \right|}}{3} = 10.\)
Vậy \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {SA} } \right| = 2\frac{{SG}}{{\sqrt 3 }} = \frac{{20}}{{\sqrt 3 }} \approx 11,5\left( {\rm{N}} \right).\)
Đáp án: 11,5.
Lời giải
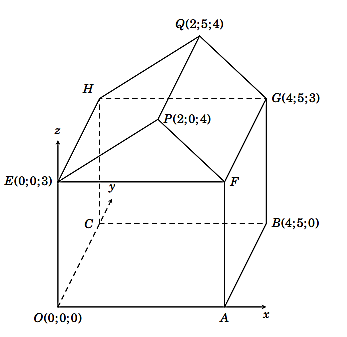
a) Sai. Vì nền nhà là hình chữ nhật nên tứ giác \(OABC\) là hình chữ nhật, suy ra \({x_A} = {x_B} = 4,{y_C} = {y_B} = \) 5. Do \(A\) nằm trên trục \(Ox\) nên tọa độ điểm \(A\) là \(\left( {4;0;0} \right)\).
b) Sai. Tường nhà là hình chữ nhật, suy ra \({y_H} = {y_C} = 5,{z_H} = {z_E} = 3\). Do \(H\) nằm trên mặt phẳng \(\left( {Oyz} \right)\) nên tọa độ điểm \(H\) là \(\left( {0;5;3} \right)\).
c) Sai. Để tính góc dốc của mái nhà, ta đi tính số đo góc nhị diện có cạnh là đường thẳng \(FG\), hai mặt phẳng lần lượt là \(\left( {FGQP} \right)\) và \(\left( {FGHE} \right)\). Do mặt phẳng \(\left( {Ozx} \right)\) vuông góc với hai mặt phẳng \(\left( {FGQP} \right)\) và \(\left( {FGHE} \right)\) nên góc \(PFE\) là góc phẳng nhị diện ứng với góc nhị diện đó.
Ta có \(\overrightarrow {FP} = \left( { - 2;0;1} \right),\overrightarrow {FE} = \left( { - 4;0;0} \right)\).
Suy ra \({\rm{cos}}\widehat {PFE} = {\rm{cos}}\left( {\overrightarrow {FP} ,\overrightarrow {FE} } \right) = \frac{{\overrightarrow {FP} \cdot \overrightarrow {FE} }}{{\left| {\overrightarrow {FP} \left| \cdot \right|\overrightarrow {FE} } \right|}} = \frac{{\left( { - 2} \right) \cdot \left( { - 4} \right) + 0 \cdot 0 + 1 \cdot 0}}{{\sqrt {{{( - 2)}^2} + {0^2} + {1^2}} \cdot \sqrt {{{( - 4)}^2} + {0^2} + {0^2}} }} = \frac{{2\sqrt 5 }}{5}\).
Do đó, \(\widehat {PFE} \approx 26,6^\circ \). Vậy góc dốc của mái nhà khoảng \(26,6^\circ \).
d) Sai. Chiều cao bằng cao độ của điểm \(P\) suy ra \(h = 4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.