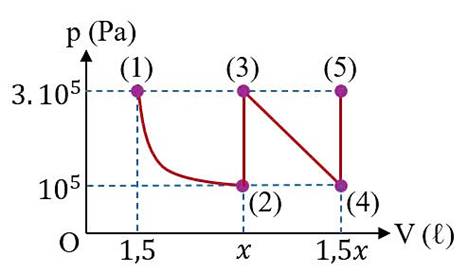
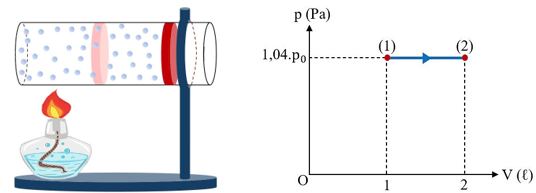
Một khối khí lí tưởng được chứa trong một xi lanh nằm ngang cố định, được đậy kín bằng một pittông có thể chuyển động. Khi khối khí trong xi lanh hấp thụ một nhiệt lượng $400\ \text{J}$, nó giãn nở và đẩy pittông di chuyển đều. Quá trình biến đổi trạng thái của khối khí được biểu diễn bằng một đồ thị $p(V)$ như hình bên dưới. Biết áp suất khí quyển là $p_0 = 10^{5}\ \text{Pa}$, tiết diện của pittông là $S = 50\ \text{cm}^{2}$.

Trong quá trình biến đổi trạng thái của khối khí từ trạng thái (1) sang trạng thái (2), độ biến thiên nội năng của khối khí bằng
Quảng cáo
Trả lời:
Đáp án đúng là D
Theo nguyên lí I nhiệt động lực học:
\[
\Delta U = A + Q.
\]
Trên đồ thị, quá trình (1) → (2) là đẳng áp với $p = 1{,}04\,p_0$, $V_1 = 1\ \ell$, $V_2 = 2\ \ell$
($1\ \ell = 10^{-3}\ \text{m}^3$). Công do khí thực hiện:
\[
A = -\,p\,\Delta V = -\,1{,}04\,p_0\,(V_2 - V_1)
= -\,1{,}04\cdot 10^5 \cdot (2-1)\cdot 10^{-3}
= -\,104\ \text{J}.
\]
Với $Q = 400\ \text{J}$:
\[
\Delta U = A + Q = -104 + 400 = 296\ \text{J}.
\]
Câu hỏi cùng đoạn
Câu 2:
Lực ma sát giữa pittông và thành xi lanh có độ lớn bằng
Đáp án đúng là C
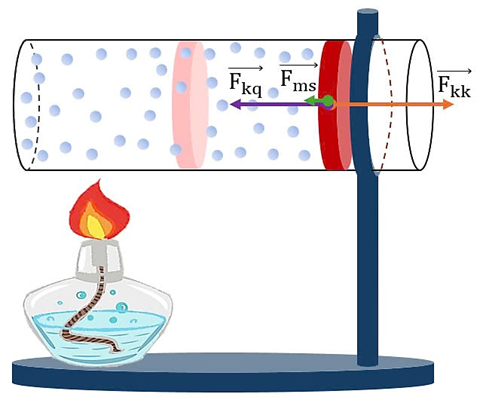
Xét theo phương chuyển động của pittông (pittông chuyển động đều nên $a=0$). Gọi lực do khí trong xi lanh tác dụng lên pittông là $F_{\text{kh}}=pS$, lực do khí quyển là $F_{\text{kq}}=p_0S$, và lực ma sát là $F_{\text{ms}}$.
Theo định luật II Newton:
\[
F_{\text{kh}} - F_{\text{kq}} - F_{\text{ms}} = m a = 0
\quad\Rightarrow\quad
F_{\text{ms}} = F_{\text{kh}} - F_{\text{kq}} = (p-p_0)S.
\]
Từ đồ thị trạng thái: $p = 1{,}04\,p_0$, với $p_0 = 10^{5}\ \text{Pa}$, $S = 50\ \text{cm}^2 = 50\times 10^{-4}\ \text{m}^2$:
\[
F_{\text{ms}}=(1{,}04\,p_0 - p_0)S
= 0{,}04\,p_0\,S
= 0{,}04\times 10^{5}\times 50\times 10^{-4}
= 20\ \text{N}.
\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là B
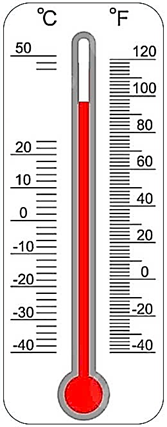
Vì thủy ngân giãn nở tuyến tính theo nhiệt độ, nên khi nhiệt độ tăng thêm $1^\circ\text{C}$ thì chiều dài cột thủy ngân tăng một đoạn
\[
\Delta \ell_{1^\circ\text{C}}=\frac{6{,}25}{50}=0{,}125\ \text{cm}.
\]
Khoảng cách từ vạch $0^\circ\text{C}$ đến mức thủy ngân là $4{,}5\ \text{cm}$, do đó nhiệt độ là
\[
t=\frac{4{,}5}{0{,}125}=36^\circ\text{C}.
\]
Câu 2
Lời giải
Đáp án đúng là B
Do nhiệt độ đo được là hàm bậc nhất theo chiều dài cột thủy ngân nên ta có: $t = a\,\ell + b$.
Khi $t = 0^\circ\text{C}$, $\ell = 2\ \text{cm}$:
\[
0 = a\cdot 2 + b \;\Leftrightarrow\; 2a + b = 0 \quad (1)
\]
Khi $t = 100^\circ\text{C}$, $\ell = 22\ \text{cm}$:
\[
100 = a\cdot 22 + b \;\Leftrightarrow\; 22a + b = 100 \quad (2)
\]
Từ (1) và (2) suy ra hệ:
\[
\begin{cases}
2a + b = 0,\\
22a + b = 100
\end{cases}
\Rightarrow a = 5,\quad b = -10.
\]
Vậy $t = 5\ell - 10$. Với $\ell = 18\ \text{cm}$:
\[
t = 5\cdot 18 - 10 = 80^\circ\text{C}.
\]
Câu 3
A. nhận một công bằng 270 J.
B. nhận một công bằng 70 J.
C. thực hiện một công bằng 70 J.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
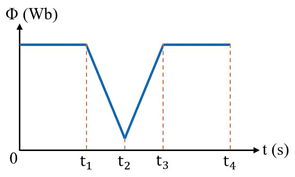
A. Từ t = 0 đến t = t2.
B. Từ t = t1 đến t = t2.
C. Từ t = t2 đến t = t4.
D. Từ t = 0 đến t = t1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.