Trong một kì thi, hai trường A, B có tổng cộng 350 học sinh dự thi. Kết quả hai trường đó có 338 học sinh trúng tuyển. Tính ra thì trường A có 97% và trường B có 96% số học sinh trúng tuyển. Hỏi trường B có bao nhiêu học sinh dự thi.
a) Tỉ lệ trúng tuyển của trường A cao hơn trường B.
b) Số học không trúng tuyển của hai trường là 12 học sinh.
c) Phương trình thể hiện số học sinh trúng tuyển của hai trường đạt là \[97x + 96y = 338.\]
d) Trường A có 150 thí sinh dự thi.
Trong một kì thi, hai trường A, B có tổng cộng 350 học sinh dự thi. Kết quả hai trường đó có 338 học sinh trúng tuyển. Tính ra thì trường A có 97% và trường B có 96% số học sinh trúng tuyển. Hỏi trường B có bao nhiêu học sinh dự thi.
a) Tỉ lệ trúng tuyển của trường A cao hơn trường B.
b) Số học không trúng tuyển của hai trường là 12 học sinh.
c) Phương trình thể hiện số học sinh trúng tuyển của hai trường đạt là \[97x + 96y = 338.\]
d) Trường A có 150 thí sinh dự thi.
Quảng cáo
Trả lời:
Gọi số học sinh dự thi của hai trường A, B lần lượt là \[x,{\rm{ }}y{\rm{ }}\left( {0 < x,{\rm{ }}y < 350} \right)\] (học sinh).
a) Đúng. Vì trường A có 97% và trường B có 96% số học sinh trúng tuyển nên tỉ lệ trúng tuyển của trường A cao hơn trường B.
b) Đúng. Theo đề bài, hai trường A, B có tổng cộng 350 học sinh dự thi và có 338 học sinh trúng tuyển.
Do đó, số học không trúng tuyển của hai trường là: \[350 - 338 = 12\] (học sinh).
c) Sai. Vì trường A có 97% và trường B có 96% số học sinh trúng tuyển và cả hai trường đó có 338 học sinh trúng tuyển nên ta có phương trình \[97\% x + 96\% y = 338.\]
d) Sai. Vì hai trường A, B có tổng cộng 350 học sinh dự thi nên ta có phương trình
\[x + y = 350\] (học sinh).
Từ đó, ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 350\\97\% x + 96\% y = 338\end{array} \right.\).
Nhân hai vế của phương trình thứ hai với 100, ta được hệ \(\left\{ \begin{array}{l}x + y = 350\\97x + 96y = 33\,\,800\end{array} \right.\).
Từ phương trình thứ nhất của hệ mới, ta có: \[y = 350 - x.\] Thế vào phương trình thứ hai của hệ, ta được: \[97x + 96\left( {350 - x} \right) = 33\,\,800\] hay \[97x + 33\,\,600 - 96x = 33\,\,800\] nên \[x = 200.\]
Từ đó \[y = 350 - 200 = 150.\]
Vậy trường A có 200 thí sinh dự thi.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng. Phương trình \(x - y = m + 1\) là phương trình bậc nhất hai ẩn với \(a = 1\,;\,\,b = - 1\,;\,\,c = m + 1\)(\(m\) là tham số).
b) Sai. Với \(m = 2\) ta có hệ phương trình \(\left\{ \begin{array}{l}x - y = 3\\2x + y = 12\end{array} \right.\).
Cộng vế theo vế của hai phương trình của hệ mới, ta được \(3x = 15\) nên \(x = 5\).
Từ đó \(5 - y = 3\) nên \(y = 2\).
Vậy nghiệm của hệ phương trình khi \(m = 2\) là \((x\,;\,\,y) = \left( {5\,;\,\,2} \right).\)
c) Đúng. Cộng vế theo vế của hai phương trình của hệ đã cho, ta được \(3x = 6m + 3\) nên \(x = 2m + 1.\)
Từ đó \(2m + 1 - y = m + 1\) nên \(y = \left( {2m + 1} \right) - \left( {m + 1} \right) = m.\)
d) Đúng. Để hệ phương trình có nghiệm thỏa mãn \(x > 1\,;\,\,y < 2\) thì
\(\left\{ \begin{array}{l}2m + 1 > 1\\m < 2\end{array} \right.\) nên \(\left\{ \begin{array}{l}m > 0\\m < 2\end{array} \right.\) hay \(0 < m < 2\).Lời giải
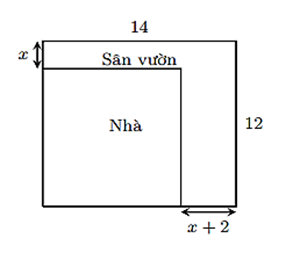
Diện tích làm nhà là: \[\left( {12 - x} \right)\left[ {14 - \left( {x + 2} \right)} \right] = \left( {12 - x} \right)\left( {12 - x} \right)\,\,\,({{\rm{m}}^{\rm{2}}})\] (điều kiện \(0 < x < 12\)).
Vì diện tích đất làm nhà là \(100\,\,{{\rm{m}}^{\rm{2}}}\) nên ta có phương trình
\(\left( {12 - x} \right)\left( {12 - x} \right)\, = 100\)
\({\left( {12 - x} \right)^2} - {10^2} = 0\)
\(\left( {12 - x - 10} \right)\left( {12 - x + 10} \right) = 0\)
\(\left( {2 - x} \right)\left( {22 - x} \right) = 0\)
\(2 - x = 0\) hoặc \(22 - x = 0\)
\(x = 2\) (TMĐK) hoặc \(x = 22\) (loại)
Vậy \(x = 2\,\,{\rm{m}}\).
Đáp án: 2Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\left\{ \begin{array}{l}x + y = 3,5\\130x + 50y = 295\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x - y = 3,5\\130x + y = 295\end{array} \right.\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.