Một công nhân dự kiến làm \[33\] sản phẩm trong một thời gian nhất định. Trước khi thực hiện, xí nghiệp giao thêm cho công nhân đó \[29\] sản phẩm nữa. Do đó mặc dù mỗi giờ công nhân đó đã làm thêm \[3\] sản phẩm nhưng vẫn hoàn thành chậm hơn dự kiến \[1\] giờ \[30\] phút. Năng suất dự kiến của công nhân đó là bao nhiêu sản phẩm/giờ?
Quảng cáo
Trả lời:
Gọi năng suất dự kiến của người công nhân là \[x\] (sản phẩm/giờ, \[x \in {\mathbb{N}^ * })\].
Năng suất thực tế của người công nhân là \[x + 3\] (sản phẩm/giờ).
Thời gian công nhân làm hết 33 sản phẩm theo dự kiến là \[\frac{{33}}{x}\] (giờ).
Số sản phẩm người công nhân được giao trên thực tế là: \[33 + 29 = 62\] (sản phẩm).
Thời gian người công nhân đó làm trên thực tế là: \[\frac{{62}}{{x + 3}}\] (giờ)
Mặc dù mỗi giờ công nhân đó đã làm thêm 3 sản phẩm những vẫn hoàn thành chậm hơn dự kiến \[1\] giờ \[30\] phút \[ = \frac{3}{2}\] giờ, nên ta có phương trình: \[\frac{{62}}{{x + 3}} - \frac{{33}}{x} = \frac{3}{2}\].
Giải phương trình:
\[\frac{{62 \cdot 2x}}{{2x\left( {x + 3} \right)}} - \frac{{33 \cdot 2\left( {x + 3} \right)}}{{2x\left( {x + 3} \right)}} = \frac{{3x\left( {x + 3} \right)}}{{2x\left( {x + 3} \right)}}\]
\[62 \cdot 2x - 33 \cdot 2\left( {x + 3} \right) = 3x\left( {x + 3} \right)\]
\[124x - 66x - 198 = 3{x^2} + 9x\]
\[3{x^2} - 49x + 198 = 0\]
\[3{x^2} - 27x - 22x + 198 = 0\]
\[3x\left( {x - 9} \right) - 22\left( {x - 9} \right) = 0\]
\[\left( {x - 9} \right)\left( {3x - 22} \right) = 0\]
\[3x - 22 = 0\] hoặc \[x - 9 = 0\]
\[3x = 22\] hoặc \[x = 9\]
\[x = \frac{{22}}{3}\] (không thỏa mãn) hoặc \[x = 9\] (thỏa mãn).
Do đó, năng suất dự kiến của công nhân đó là \[9\] (sản phẩm/giờ).
Đáp án: 9.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng. Phương trình \(x - y = m + 1\) là phương trình bậc nhất hai ẩn với \(a = 1\,;\,\,b = - 1\,;\,\,c = m + 1\)(\(m\) là tham số).
b) Sai. Với \(m = 2\) ta có hệ phương trình \(\left\{ \begin{array}{l}x - y = 3\\2x + y = 12\end{array} \right.\).
Cộng vế theo vế của hai phương trình của hệ mới, ta được \(3x = 15\) nên \(x = 5\).
Từ đó \(5 - y = 3\) nên \(y = 2\).
Vậy nghiệm của hệ phương trình khi \(m = 2\) là \((x\,;\,\,y) = \left( {5\,;\,\,2} \right).\)
c) Đúng. Cộng vế theo vế của hai phương trình của hệ đã cho, ta được \(3x = 6m + 3\) nên \(x = 2m + 1.\)
Từ đó \(2m + 1 - y = m + 1\) nên \(y = \left( {2m + 1} \right) - \left( {m + 1} \right) = m.\)
d) Đúng. Để hệ phương trình có nghiệm thỏa mãn \(x > 1\,;\,\,y < 2\) thì
\(\left\{ \begin{array}{l}2m + 1 > 1\\m < 2\end{array} \right.\) nên \(\left\{ \begin{array}{l}m > 0\\m < 2\end{array} \right.\) hay \(0 < m < 2\).Lời giải
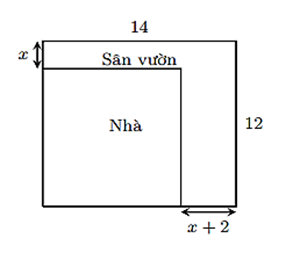
Diện tích làm nhà là: \[\left( {12 - x} \right)\left[ {14 - \left( {x + 2} \right)} \right] = \left( {12 - x} \right)\left( {12 - x} \right)\,\,\,({{\rm{m}}^{\rm{2}}})\] (điều kiện \(0 < x < 12\)).
Vì diện tích đất làm nhà là \(100\,\,{{\rm{m}}^{\rm{2}}}\) nên ta có phương trình
\(\left( {12 - x} \right)\left( {12 - x} \right)\, = 100\)
\({\left( {12 - x} \right)^2} - {10^2} = 0\)
\(\left( {12 - x - 10} \right)\left( {12 - x + 10} \right) = 0\)
\(\left( {2 - x} \right)\left( {22 - x} \right) = 0\)
\(2 - x = 0\) hoặc \(22 - x = 0\)
\(x = 2\) (TMĐK) hoặc \(x = 22\) (loại)
Vậy \(x = 2\,\,{\rm{m}}\).
Đáp án: 2Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\left\{ \begin{array}{l}x + y = 3,5\\130x + 50y = 295\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x - y = 3,5\\130x + y = 295\end{array} \right.\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.