Tập nghiệm của bất phương trình \({x^2} - 9 \le 0\) là
Quảng cáo
Trả lời:
\({x^2} - 9 \le 0\)\( \Leftrightarrow - 3 \le x \le 3\).
Vậy tập nghiệm của bất phương trình là \(S = \left[ { - 3;3} \right]\). Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) triệu đồng là số tiền mà doanh nghiệp A dự định giảm giá \(\left( {0 \le x \le 4} \right)\).
Khi đó:
Lợi nhuận thu được khi bán một chiếc tủ lạnh là \(31 - x - 27 = 4 - x\).
Số xe mà doanh nghiệp sẽ bán được trong một năm là \(600 + 200x\).
Lợi nhuận mà doanh nghiệp sẽ bán được trong một năm là
\(f\left( x \right) = \left( {4 - x} \right)\left( {600 + 200x} \right)\)\( \Leftrightarrow f\left( x \right) = - 200{x^2} + 200x + 2400\).
Xét hàm số \(f\left( x \right) = - 200{x^2} + 200x + 2400\) trên đoạn \(\left[ {0;4} \right]\) có bảng biến thiên
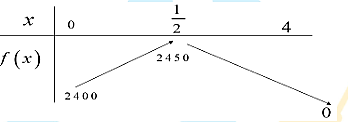
Vậy giá trị lớn nhất của hàm số \(f\left( x \right)\) bằng 2450 triệu khi \(x = \frac{1}{2}\).
Vậy giá mới của chiếc xe là 30,5 triệu đồng thì lợi nhuân thu được là cao nhất.
Lời giải
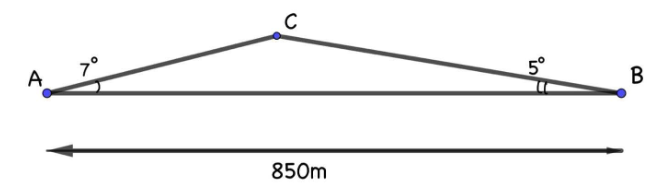
Đổi \(4{\rm{km/h = }}\frac{{200}}{3}\)m/phút; \({\rm{19km/h = }}\frac{{950}}{3}\)m/phút.
Có \(\widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right) = 180^\circ - \left( {7^\circ + 5^\circ } \right) = 168^\circ \).
Áp dụng định lí sin ta có: \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\).
Suy ra \(AC = \frac{{AB.\sin B}}{{\sin C}} = \frac{{850.\sin 5^\circ }}{{\sin 168^\circ }}\); \(BC = \frac{{AB.\sin A}}{{\sin C}} = \frac{{850.\sin 7^\circ }}{{\sin 168^\circ }}\).
Thời gian đi từ nhà đến trường là \(\frac{{AC}}{{\frac{{200}}{3}}} + \frac{{BC}}{{\frac{{950}}{3}}} = \frac{{3.850.\sin 5^\circ }}{{200.\sin 168^\circ }} + \frac{{3.850.\sin 7^\circ }}{{950.\sin 168^\circ }} \approx 7\) phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.