Để đo chiều cao của một bức tường Điệp dùng một quyển sách và ngắm sao cho hai cạnh bia của quyển sách hướng về vị trí cao nhất và vị trí thấp nhất của bức tường (tham khảo hình vẽ). Biết rằng Điệp đứng cách tường \(1,5\;\,{\rm{m}}\) và vị trí mắt khi quan sát cách mặt đất là \(1,2\;\,{\rm{m}}\).
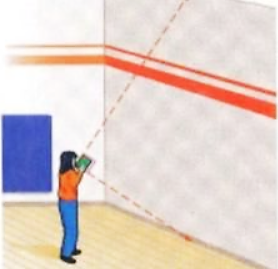
Hỏi chiều cao của bức tường là bao nhiêu? (kết quả làm tròn đến hàng đơn vị).

Hỏi chiều cao của bức tường là bao nhiêu? (kết quả làm tròn đến hàng đơn vị).
Câu hỏi trong đề: Đề kiểm tra Toán 9 Cánh diều Chương 4 có đáp án !!
Quảng cáo
Trả lời:
Chọn C
Gọi \(A,\,\,D\) là vị trí của người đứng;
\(C,\,\,D\) là vị trí bức tường phía trên và dưới cùng;
\[H\] là hình chiếu của \[A\] lên \[BC.\]
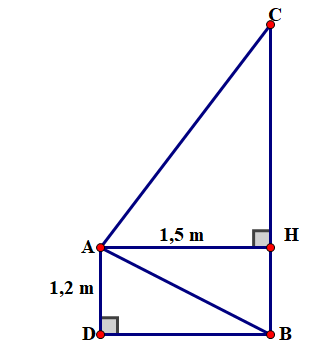
Tứ giác \[ADBH\] là hình chữ nhật nên \(BD = AH = 1,5\;\,{\rm{m}}\);
\[BH = AD = 1,2\;\,{\rm{m}}{\rm{.}}\]
Áp dụng định lí Pythagore vào tam giác \(ABD\) vuông tại \(D,\) ta có:
\(A{B^2} = A{D^2} + B{D^2} = 1,{2^2} + 1,{5^2} = 3,69\).
Suy ra \(AB = \sqrt {3,69} = 1,92\;\,({\rm{m}}).\)
Xét \(\Delta ABC\) vuông tại \[A,\] đường cao \[AH,\] ta có:
\(A{B^2} = BH \cdot BC\) hay \(BC = \frac{{A{B^2}}}{{BH}} = \frac{{3,69}}{{1,2}} \approx 3\;\,\,({\rm{m}})\).
Vậy chiều cao của bức tường là \[3{\rm{ m}}.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Xét \(\Delta ABH\) vuông tại \(A\), ta có:
\(\tan B = \frac{{AH}}{{AB}}\) hay \(\tan 63^\circ = \frac{{AH}}{{235}}\) nên \(AH = 235 \cdot \tan 63^\circ = 461\;\,({\rm{m)}}\).
Vậy chiều cao của tòa nhà này là \[461{\rm{ m}}.\]
Đáp án: 461.
Lời giải
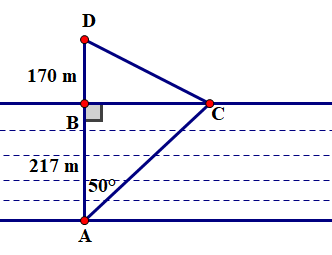
• Xét \(\Delta ABC\) vuông tại \(B\), ta có:
\(\tan A = \frac{{BC}}{{AB}}\) hay \(\tan 50^\circ = \frac{{BC}}{{217}}\) nên \(BC = 217 \cdot \tan 50^\circ = 258,6\;\,({\rm{m)}}\).
\(AC = \sqrt {A{B^2} + {B^2}} = \sqrt {{{217}^2} + 258,{6^2}} = 337,6\;\,({\rm{m)}}\).
• Xét \(\Delta BDC\) vuông tại \(B\), ta có:
\(DC = \sqrt {B{C^2} + B{D^2}} = \sqrt {{{170}^2} + 258,{6^2}} = 309,5\;\,({\rm{m)}}\).
\(AC + DC = 337,6 + 309,5 = 647\,\;({\rm{m)}}{\rm{.}}\)
Vậy quãng đường mà Hùng đã đi từ \(A\) đến \(D\) là \(647\,\;{\rm{m}}\).
Đáp án: 647.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Lời giải Xét \(\Delta ABH\) vuông tại \(A\), ta có: \(\tan B = \frac{{AH}}{{AB}}\) hay \(\tan 63^\circ = \frac{{AH}}{{235}}\) nên \(AH = 235 \cdot \tan 63^\circ = 461\;\,({\rm{m)}}\). Vậy chiều cao của tòa nhà này là \[461{\rm{ m}}.\] Đáp án: 461. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/67-1761202758.png)
![Để xác định khoảng cách từ một gốc cây \[A\] trên một hòn đảo nh (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/43-1761183381.png)