Phần 3. Trắc nghiệm trả lời ngắn
Trong mỗi câu hỏi, thí sinh viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
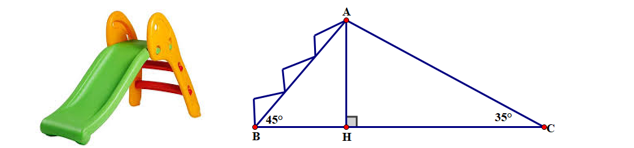
Tòa nhà Landmart 81 là một tòa nhà cao tầng ngay bên bờ sông Sài Gòn tại TP. Hồ Chí Minh. Tòa nhà này có 81 tầng, cao nhất Đông Nam Á (năm 2018). Ý tưởng thiết kế của The Landmark 81 được lấy cảm hứng từ những bó tre truyền thống tượng trưng cho sức mạnh và sự đoàn kết trong văn hóa Việt Nam. Tại một thời điểm tia sáng mặt trời tạo với mặt đất một góc là \(63^\circ \) (góc B) thì người ta đo được bóng của tòa nhà trên mặt đất dài khoảng \[235{\rm{ m}}\] (độ dài \[AB).\] Hãy ước tính chiều cao của tòa nhà này (đoạn thẳng \[AH\]) (làm tròn kết quả đến chữ số thập phân thứ nhất).
![Lời giải Xét \(\Delta ABH\) vuông tại \(A\), ta có: \(\tan B = \frac{{AH}}{{AB}}\) hay \(\tan 63^\circ = \frac{{AH}}{{235}}\) nên \(AH = 235 \cdot \tan 63^\circ = 461\;\,({\rm{m)}}\). Vậy chiều cao của tòa nhà này là \[461{\rm{ m}}.\] Đáp án: 461. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/67-1761202758.png)
Phần 3. Trắc nghiệm trả lời ngắn
Trong mỗi câu hỏi, thí sinh viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tòa nhà Landmart 81 là một tòa nhà cao tầng ngay bên bờ sông Sài Gòn tại TP. Hồ Chí Minh. Tòa nhà này có 81 tầng, cao nhất Đông Nam Á (năm 2018). Ý tưởng thiết kế của The Landmark 81 được lấy cảm hứng từ những bó tre truyền thống tượng trưng cho sức mạnh và sự đoàn kết trong văn hóa Việt Nam. Tại một thời điểm tia sáng mặt trời tạo với mặt đất một góc là \(63^\circ \) (góc B) thì người ta đo được bóng của tòa nhà trên mặt đất dài khoảng \[235{\rm{ m}}\] (độ dài \[AB).\] Hãy ước tính chiều cao của tòa nhà này (đoạn thẳng \[AH\]) (làm tròn kết quả đến chữ số thập phân thứ nhất).
Câu hỏi trong đề: Đề kiểm tra Toán 9 Cánh diều Chương 4 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Xét \(\Delta ABH\) vuông tại \(A\), ta có:
\(\tan B = \frac{{AH}}{{AB}}\) hay \(\tan 63^\circ = \frac{{AH}}{{235}}\) nên \(AH = 235 \cdot \tan 63^\circ = 461\;\,({\rm{m)}}\).
Vậy chiều cao của tòa nhà này là \[461{\rm{ m}}.\]
Đáp án: 461.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[2{\rm{ m}}.\]
B. \[8{\rm{ m}}.\]
C. \[3{\rm{ m}}.\]
D. \[8{\rm{ m}}.\]
Lời giải
Chọn C
Gọi \(A,\,\,D\) là vị trí của người đứng;
\(C,\,\,D\) là vị trí bức tường phía trên và dưới cùng;
\[H\] là hình chiếu của \[A\] lên \[BC.\]
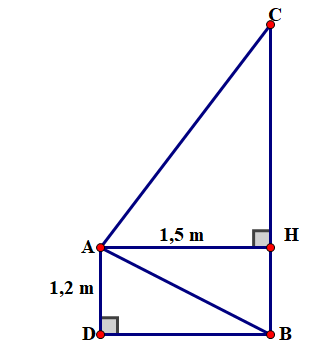
Tứ giác \[ADBH\] là hình chữ nhật nên \(BD = AH = 1,5\;\,{\rm{m}}\);
\[BH = AD = 1,2\;\,{\rm{m}}{\rm{.}}\]
Áp dụng định lí Pythagore vào tam giác \(ABD\) vuông tại \(D,\) ta có:
\(A{B^2} = A{D^2} + B{D^2} = 1,{2^2} + 1,{5^2} = 3,69\).
Suy ra \(AB = \sqrt {3,69} = 1,92\;\,({\rm{m}}).\)
Xét \(\Delta ABC\) vuông tại \[A,\] đường cao \[AH,\] ta có:
\(A{B^2} = BH \cdot BC\) hay \(BC = \frac{{A{B^2}}}{{BH}} = \frac{{3,69}}{{1,2}} \approx 3\;\,\,({\rm{m}})\).
Vậy chiều cao của bức tường là \[3{\rm{ m}}.\]
Lời giải
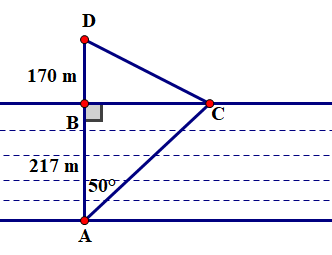
• Xét \(\Delta ABC\) vuông tại \(B\), ta có:
\(\tan A = \frac{{BC}}{{AB}}\) hay \(\tan 50^\circ = \frac{{BC}}{{217}}\) nên \(BC = 217 \cdot \tan 50^\circ = 258,6\;\,({\rm{m)}}\).
\(AC = \sqrt {A{B^2} + {B^2}} = \sqrt {{{217}^2} + 258,{6^2}} = 337,6\;\,({\rm{m)}}\).
• Xét \(\Delta BDC\) vuông tại \(B\), ta có:
\(DC = \sqrt {B{C^2} + B{D^2}} = \sqrt {{{170}^2} + 258,{6^2}} = 309,5\;\,({\rm{m)}}\).
\(AC + DC = 337,6 + 309,5 = 647\,\;({\rm{m)}}{\rm{.}}\)
Vậy quãng đường mà Hùng đã đi từ \(A\) đến \(D\) là \(647\,\;{\rm{m}}\).
Đáp án: 647.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[\alpha = 60^\circ \].
B. \[\alpha = 45^\circ \].
C. \[\alpha = 40^\circ \].
D. \[\alpha = 30^\circ \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
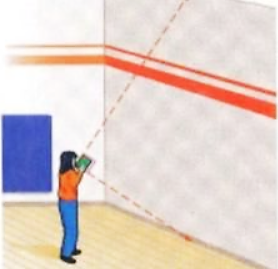
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Để xác định khoảng cách từ một gốc cây \[A\] trên một hòn đảo nh (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/43-1761183381.png)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo