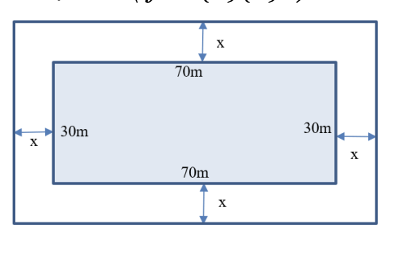
Cho tam giác \[ABC\] có ba góc nhọn \[\left( {AB\; < AC} \right).\] Đường tròn tâm \[O\] đường kính \[BC\] cắt hai cạnh \[AB,\,\,\;AC\] lần lượt tại \[E\] và \[F\] \[(E\] khác \[B,\,\,F\] khác \[C).\] Các đoạn thẳng \[BF\] và \[CE\] cắt nhau tại \[H,\] tia \[AH\] cắt \[BC\] tại \[K.\]
1) Chứng minh bốn điểm \(\widehat {BEC} = \widehat {BFC} = 90^\circ \) từ đó suy ra tứ giác \[AEHF\] nội tiếp.
2) Gọi \[D\] là giao điểm của \[AH\] và \[\left( O \right)\] \[(D\] nằm giữa \[A\] và \[H),\] chứng minh \[B{D^2}\; = BK \cdot BC\] và \(\widehat {BDH} = \widehat {BFD}.\)
3) Trong trường hợp \(\widehat {BAC} = 60^\circ \) và \(BC = 6\,\,{\rm{cm}},\)tính độ dài đoạn thẳng \[EF\] và bán kính đường tròn ngoại tiếp tam giác \[AEF.\]
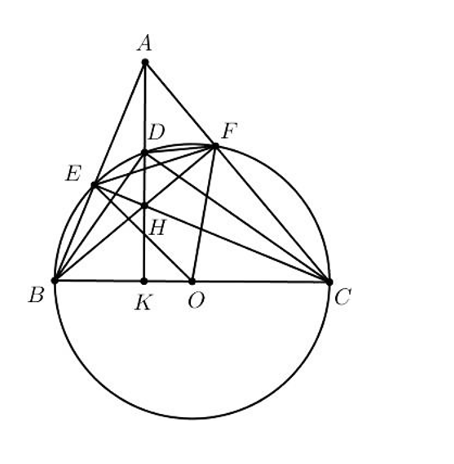
Cho tam giác \[ABC\] có ba góc nhọn \[\left( {AB\; < AC} \right).\] Đường tròn tâm \[O\] đường kính \[BC\] cắt hai cạnh \[AB,\,\,\;AC\] lần lượt tại \[E\] và \[F\] \[(E\] khác \[B,\,\,F\] khác \[C).\] Các đoạn thẳng \[BF\] và \[CE\] cắt nhau tại \[H,\] tia \[AH\] cắt \[BC\] tại \[K.\]
1) Chứng minh bốn điểm \(\widehat {BEC} = \widehat {BFC} = 90^\circ \) từ đó suy ra tứ giác \[AEHF\] nội tiếp.
2) Gọi \[D\] là giao điểm của \[AH\] và \[\left( O \right)\] \[(D\] nằm giữa \[A\] và \[H),\] chứng minh \[B{D^2}\; = BK \cdot BC\] và \(\widehat {BDH} = \widehat {BFD}.\)
3) Trong trường hợp \(\widehat {BAC} = 60^\circ \) và \(BC = 6\,\,{\rm{cm}},\)tính độ dài đoạn thẳng \[EF\] và bán kính đường tròn ngoại tiếp tam giác \[AEF.\]

Quảng cáo
Trả lời:
1) Vì \[\widehat {BEC},\,\,\widehat {BFC}\] là các góc nội tiếp chắn nửa đường tròn \(\left( O \right)\) nên ta co
Khi đó \[\Delta AEH\] vuông tại \[E\] nên \[A,\,\,E,\,\,H\] cùng thuộc đường tròn đường kính \[AH.\]
Tương tự \[\Delta AFH\]vuông tại F nên \[A,\,\,H,\,\,F\] cùng thuộc đường tròn đường kính \[AH.\]Vậy \[A,\,\,E,\,\,F,\,\,H\] cùng thuộc đường trong đường kính \[AH\] hay tứ giác \[AEHF\] nội tiếp.
2) Ta có (tính chất góc nội tiếp chắn nửa đường tròn)
Xét BDK và BCD có \[\widehat {CBD}\] chung; \[\widehat {BKD} = \;\widehat {BDC}\,\,\left( { = \;90^\circ } \right)\]
Do đó
Suy ra \(\frac{{BD}}{{BC}} = \frac{{BK}}{{BD}}\) hay \[B{D^2} = BK \cdot BC\].
Do nên \[\widehat {BDH} = \;\widehat {BCD}\] (hai góc tương ứng).
Mà \[\widehat {BCD} = \widehat {BFD}\] (hai góc nội tiếp cùng chắn cung \[BD)\]
Nên \[\widehat {BDH} = \widehat {BFD}\] (đpcm)
Do \[\Delta AFB\] vuông tại \[F\] nên \[\widehat {ABF} = 90^\circ - \widehat {BAF} = 90^\circ - 60^\circ = 30^\circ \].
Mà nên \[\widehat {OEF} = 2 \cdot 30^\circ = 60^\circ .\]
Xét \[\Delta OEF\] cân tại \[O\] (do \[OE = OF\]) có \[\widehat {EOF} = 60^\circ \] nên \[\Delta OEF\] là tam giác đều.
Suy ra \[EF = OE = OF = \frac{1}{2}BC = 3\,\,{\rm{cm}}{\rm{.}}\]
Xét \[\Delta ABC\] có đường cao \[CE\] và \[BF\] cắt nhau tại \[H\] nên \[H\] là trực tâm.
Suy ra \[AH \bot BC\]
Xét \[\Delta AHF\] và \[\widehat {BHK}\] có \[\widehat {AHF} = \;\widehat {BHK}\] (đối đỉnh) và \[\widehat {AFH} = \;\widehat {BKH}\,\,\left( { = \;90^\circ } \right)\]
Suy ra \[\widehat {HAF} = \widehat {HBK}\] hay \[\widehat {HAF} = \widehat {FBC}\]
Kết hợp \[\widehat {AFH} = \;\widehat {BFC}\,\,\left( { = \;90^\circ } \right)\] suy ra
Suy ra \(\frac{{AH}}{{BC}} = \frac{{AF}}{{BF}} = \cot \widehat {FAB} = \cot 60^\circ = \frac{{\sqrt 3 }}{3}\) .
Suy ra \(AH = \frac{{\sqrt 3 }}{3} \cdot BC = \frac{{\sqrt 3 }}{3} \cdot 6 = 2\sqrt 3 .\)
Xét tứ giác \[AEHF\] nội tiếp đường tròn đường kính \[AH\] nên bán kính bằng \(\frac{{2\sqrt 3 }}{2} = \sqrt 3 .\)
Vậy \[EF = 3\,\,{\rm{cm}}\] và bán kính đường tròn ngoại tiếp tam giác \[AEF\] là \(\sqrt 3 .\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1) Gọi \[a\] là số tấn hợp kim thép chứa \[10\% \] crom cần dùng \[\left( {a > 0} \right).\]
Khi đó, \[500--a\] là số tấn hợp kim thép 30% cần dùng.
Ta có \[a \cdot 10\% + \left( {500--a} \right) \cdot 30\% = 500 \cdot 16\% \]
\[10a + \left( {500--a} \right) \cdot 30 = 500 \cdot 16\]
\[a + 1\,\,500--3a = 800\]
\[2a = 700\]
\[a = 350\] (TMĐK)
Vậy số hợp kim thép chứa \[10\% \] crom cần dùng là 350 tấn, số hợp kim thép chứa \[30\% \] cần dùng là 150 tấn.
2) Số crôm từ 100 tấn thép chứa \[10\% \] crôm là \[10\% \cdot 100 = 10\] (tấn)
Số crôm từ x tấn thép chứa 30% crôm là \[0,3x\] (tấn)
Tổng số tấn thép là \[100 + x\] (tấn)
Phần trăm crôm có trong tổng số tấn thép nhà máy dự định luyện ra là: \(\frac{{10 + 0,3x}}{{100 + x}} \cdot 100\,\,\left( \% \right)\)
Theo đầu bài, thép không gỉ Ferritic có chứa từ 12 đến 27 phần trăm crôm, ta có:
\(12 \le \frac{{10 + 0,3x}}{{100 + x}} \cdot 100 \le 27\)
\(1\,\,200 + 12x \le 1\,\,000 + 30x \le 2\,\,700 + 27x\)
|
Xét \[1\,\,200 + 12x \le 1\,\,000 + 30x\] \[30x - 12x \ge 1\,\,200 - 1\,\,000\] \[18x \ge 200\] \[x \ge \frac{{100}}{9} & \left( 1 \right)\] |
Xét \[1\,\,000 + 30x \le 2\,\,700 + 27x\] \[30x - 27x \le 2\,\,700 - 1\,\,000\] \[3x \le 1\,\,700\] \[x \le \frac{{1\,\,700}}{3} & \left( 2 \right)\] |
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \[\frac{{100}}{9} \le x \le \frac{{1\,\,700}}{3}.\]
Vậy \[x\] nằm trong khoảng \[\frac{{100}}{9}\] đến \[\frac{{1\,\,700}}{3}.\]
Lời giải
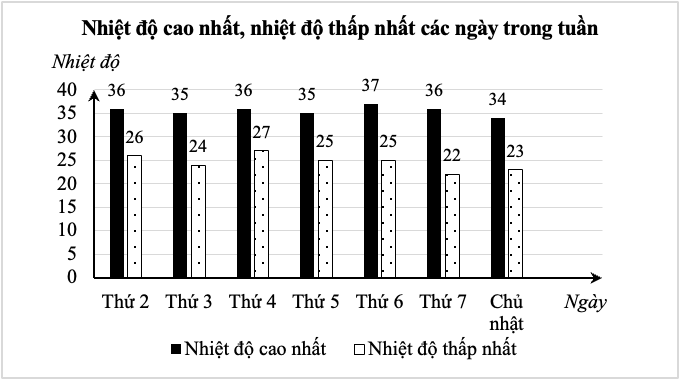
1) Dựa vào biểu đồ cột kép, ta có biên độ nhiệt của các ngày trong tuần là:
Thứ 2: \[36 - 26 = 10,\] thứ 3: \[35 - 24 = 11,\] thứ 4: \[36 - 27 = 9;\] thứ 5: \[35 - 25 = 10;\]
Thứ 6: \[37 - 25 = 12;\] thứ 7: \[36 - 22 = 14;\] chủ nhật: \[34 - 23 = 11.\]
Vậy ngày có biên độ nhiệt lớn nhất trong tuần của thành phố Hồ Chí Minh là thứ 7.
2) Ta có số ngày có nhiệt độ cao không quá 35 độ C là 3 (ngày).
Suy ra số phần tử của biến cố A là 3.
Xác suất để ngày được chọn có nhiệt độ cao nhất không quá 35 độ C là \(\frac{3}{7}\).
Có số ngày có biên độ nhiệt nhỏ hơn 12 độ C là 5 (ngày).
Suy ra số phần tử của biến cố B là 5.
Xác suất để ngày được chọn có biên độ nhiệt nhỏ hơn 12 độ C là \(\frac{5}{7}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Một quả dưa hấu không hạt ruột đỏ dạng hình cầu có đường kính 25cm và phần vỏ dày 2 cm] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/anh-man-hinh-2025-10-24-luc-200412-1761310950.png)