Trong một cuộc thi pha chế đồ uống gồm hai loại là \(A\) và \(B\), mỗi đội chơi được sử dụng tối đa \(24\;g\) hương liệu, 9 cốc nước lọc và \(210\;g\) đường. Để pha chế 1 cốc đồ uống loại \(A\) cần 1 cốc nước lọc, \(30\;g\) đường và \(1\;g\) hương liệu. Để pha chế 1 cốc đồ uống loại \(B\) cần 1 cốc nước lọc, \(10\;g\) đường và \(4\;g\) hương liệu. Mỗi cốc đồ uống loại \(A\) nhận được 6 điểm thương, mỗi cốc đồ uống loại \(B\) nhận được 8 điểm thưởng. Để đạt được số điểm thưởng cao nhất, đội chơi cần pha chế bao nhiêu cốc đồ uống loại A?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 10 có đáp án !!
Quảng cáo
Trả lời:
|
Trả lời |
4 |
|
|
|
Gọi \(x,y\) lần lượt là số cốc đồ uống loại \(A\), loại \(B\) mà đội chơi cần pha chế với \(x \ge 0,y \ge 0\).
Số cốc nước cần dùng là: \(x + y\) (cốc).
Lượng đường cần dùng là: \(30x + 10y(\;g)\).
Lượng hương liệu cần dùng là: \(x + 4y(\;g)\).
Theo giả thiết, ta có: \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 9\\30x + 10y \le 210\\x + 4y \le 24\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 9\\3x + y \le 21\\x + 4y \le 24\end{array}\end{array}} \right.} \right.\left( {III} \right)\)
Số điểm thường nhận được là: \(F = 6x + 8y\).
Ta tìm giá trị lớn nhất trên miền nghiệm của hệ bất phương trình (III).
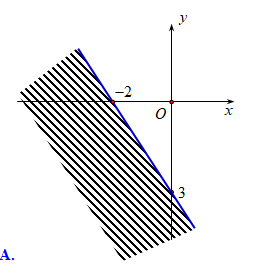
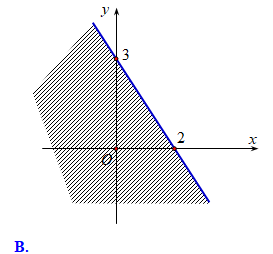
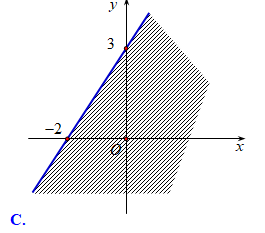
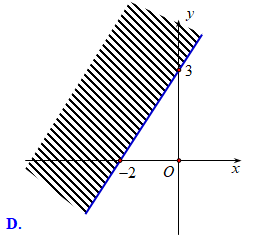
Miền nghiệm của hệ bất phương trình (III) là miền ngũ giác \(OABCD\) với \(O\left( {0;0} \right),\,A\left( {7;0} \right),\,B\left( {6;3} \right),\,C\left( {4;5} \right),\,D\left( {0;6} \right)\)(hình).
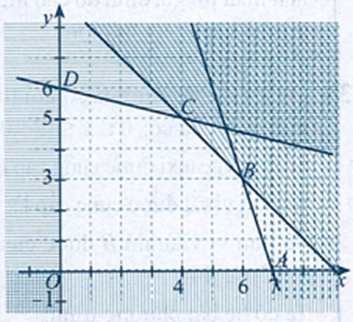
Tính giá trị của \(F = 6x + 8y\) tại các cặp số \(\left( {x;y} \right)\) là tọa độ của các đỉnh ngũ giác \(OABCD\) rồi so sánh các giá trị đó, ta được \(F\) đạt giá trị lớn nhất bằng \(64\) tại \(x = 4;y = 5\).
Vậy để đạt được số điểm thưởng cao nhất, đội chơi cần pha chế 4 cốc đồ uống loại \(A\), 5 cốc đồ uống loại \(B\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
a) |
S |
b) |
S |
c) |
S |
d) |
Đ |
(Đúng) Gọi \(x\), \(y\) (đơn vị: triệu đồng) tiền bác Minh đầu tư vào kho ta có hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y \le 240}\\{y \ge 40}\\{x \ge 3y.}\end{array}} \right.\)
(Vì): Theo giả thiết ta có hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y \le 240}\\{y \ge 40}\\{x \ge 3y.}\end{array}} \right.\)
(Sai) Miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư vào kho là một tứ giác.
(Vì): Miền nghiệm của hệ trên là miền tam giác \(ABC\) với \(A(180;60)\), \(B(120;40)\), \(C(200;40)\).
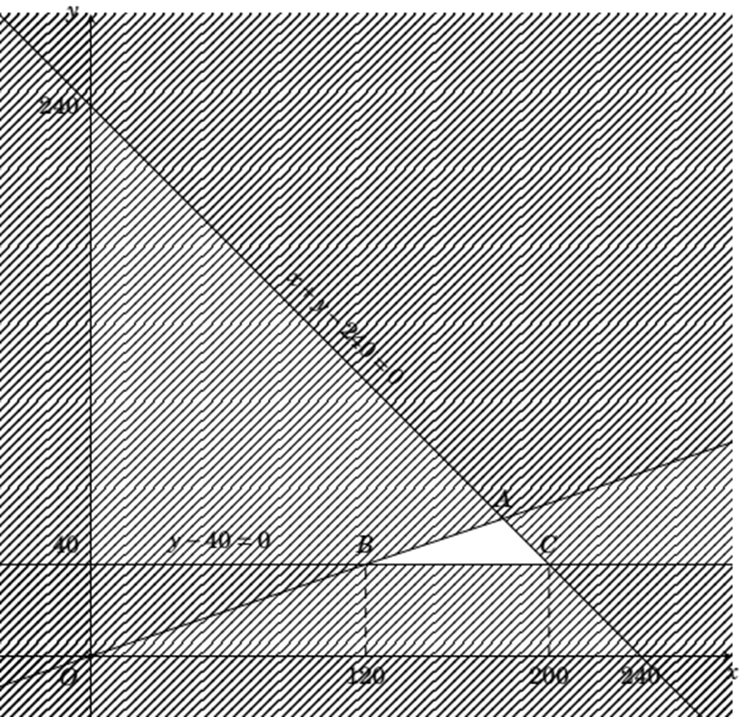
(Sai) Điểm \(C(200;40)\) không thuộc miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư vào kho.
(Vì): Điểm \(C(200;40)\) thuộc miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư vào kho.
(Sai) Điểm \(A(180;60)\) là điểm có tung độ lớn nhất thuộc miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư vào kho.
(Vì): Điểm \(A(180;60)\) là điểm có tung độ lớn nhất thuộc miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư vào kho.
Câu 2
A. \[r = \frac{{10\sqrt 3 }}{{31}}{\rm{cm}}\].
Lời giải
Chọn D
Ta có
+ \(a = \sqrt {{b^2} + {c^2} - 2bc\cos A} = \sqrt {{8^2} + {5^2} - 2.8.5.c{\rm{os6}}{{\rm{0}}^0}} = 7{\rm{cm}}\).
+ \(S = \frac{1}{2}bc\sin A = \frac{1}{2}.8.5.\sin {60^0} = 10\sqrt 3 {\rm{c}}{{\rm{m}}^2};\;\;p = \frac{{a + b + c}}{2} = \frac{{7 + 8 + 5}}{2} = 10{\rm{cm}}\)
Suy ra \(r = \frac{S}{p} = \frac{{10\sqrt 3 }}{{10}} = \sqrt 3 {\rm{cm}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(33\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.