Một gian hàng trưng bày bàn và ghế rộng 60 m2. Diện tích để kê một chiếc ghế là 0,5 m2, một chiếc bàn là 1,2 m2. Gọi \(x\) là số chiếc ghế, \(y\) là số chiếc bàn được kê. Biết diện tích mặt sàn dành cho lưu thông tối thiểu là 12 m2. Giả sử gian hàng đã kê 10 chiếc bàn thì phần diện tích cho phép còn lại có thể kê được nhiều nhất bao nhiêu chiếc ghế?
Một gian hàng trưng bày bàn và ghế rộng 60 m2. Diện tích để kê một chiếc ghế là 0,5 m2, một chiếc bàn là 1,2 m2. Gọi \(x\) là số chiếc ghế, \(y\) là số chiếc bàn được kê. Biết diện tích mặt sàn dành cho lưu thông tối thiểu là 12 m2. Giả sử gian hàng đã kê 10 chiếc bàn thì phần diện tích cho phép còn lại có thể kê được nhiều nhất bao nhiêu chiếc ghế?
Câu hỏi trong đề: Bộ 5 đề thi giữa kì 1 Toán 10 cấu trúc mới !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
Trả lời: 72
Tổng diện tích để kê \(x\) chiếc ghế, \(y\) chiếc bàn là \(0,5x + 1,2y\).
Vì diện tích mặt sàn dành cho lưu thông tối thiểu là 12 m2 nên diện tích diện tích cho gian hàng trưng bày là \(0,5x + 1,2y \le 48\).
Vì đã kê 10 chiếc bàn nên \(0,5x + 1,2.10 \le 48\)\( \Leftrightarrow x \le 72\).
Do đó có thể kê nhiều nhất 72 chiếc ghế.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Đ, b) Đ, c) Đ, d) S
a) Gọi \(x,y,\left( {x,y \ge 0} \right)\) (hecta) lần lượt là diện tích đất dùng để trồng mít và xoài.
Do bác An dự định trồng hai loại cây ăn trái là mít và xoài trong nông trại rộng 100 hecta nên \(x + y \le 100\).
b) Vì mỗi hecta trồng mít cần 20 công chăm sóc và mỗi hecta trồng xoài cần 40 công chăm sóc mà công cần dùng không được vượt quá 2 800 công nên ta có \(20x + 40y \le 2800\) hay \(x + 2y \le 140\).
c) Tổng lợi nhuận thu được là \(E = 150x + 180y\)(triệu đồng).
d) Bài toán trở thành tìm giá trị lớn nhất của \(E = 150x + 180y\) trên miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 100\\x + 2y \le 140\end{array} \right.\).
Ta có miền nghiệm của hệ bất phương trình là miền tứ giác OABC (phần tô màu).
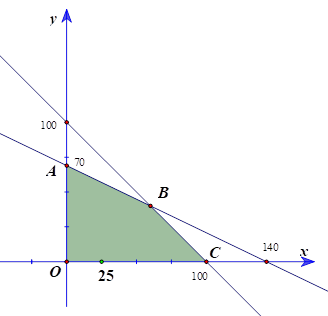
Ta có \(O\left( {0;0} \right),A\left( {0;70} \right),B\left( {60;40} \right),C\left( {100;0} \right)\).
Ta có \(E\left( {0;0} \right) = 150.0 + 180.0 = 0\); \(E\left( {0;70} \right) = 150.0 + 180.70 = 12600\);
\(E\left( {60;40} \right) = 150.60 + 180.40 = 16200\); \(E\left( {100;0} \right) = 150.100 + 180.0 = 15000\).
Vậy lợi nhuận thu được lớn nhất là 16,2 tỷ đồng.
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) S, b) Đ, c) S, d) Đ
a) 2010 không chia hết cho 4 nên mệnh đề A sai.
b) 31 là số nguyên tố nên mệnh đề B đúng.
c) mệnh đề P sai.
d) Hình thoi là hình có 4 cạnh bằng nhau nên mệnh đề Q đúng.
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\(\frac{a}{{\sin A}} = 2R\).
B. \(\sin A = \frac{a}{{2R}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[\left\{ \begin{array}{l}y \ge 0\\5x - 4y \ge 10\\5x + 4y \le 10\end{array} \right.\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(N\left( { - 1\,;1} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập