PHẦN III. Câu trắc nghiệm trả lời ngắn.Thí sinh trả lời câu 1 đến câu 6.
Một nhà phân phối bánh gạo có hai nhà kho ở phía Đông và phía Tây của thành phố. Kho ở phía Đông có \(80\) thùng bánh gạo, kho ở phía Tây có \(45\) thùng bánh gạo. Sáng thứ Hai đầu tuần, đại lí \(A\) cần \(50\) thùng bánh gạo, đại lí \(B\) cần \(70\) thùng bánh gạo. Chi phí giao hàng cho mỗi thùng bánh gạo của kho ở phía Đông là \(10\) nghìn đồng cho đại lí \(A\) và \(12\) nghìn đồng cho đại lí \(B\). Chi phí giao hàng cho mỗi thùng bánh gạo của kho ở phía Tây là \(9\) nghìn đồng cho đại lí \(A\) và \(11\) nghìn đồng cho đại lí \(B\). Chi phí vận chuyển là nhỏ nhất nhà phân phối cần phải trả là bao nhiêu nghìn đồng?
PHẦN III. Câu trắc nghiệm trả lời ngắn.Thí sinh trả lời câu 1 đến câu 6.
Một nhà phân phối bánh gạo có hai nhà kho ở phía Đông và phía Tây của thành phố. Kho ở phía Đông có \(80\) thùng bánh gạo, kho ở phía Tây có \(45\) thùng bánh gạo. Sáng thứ Hai đầu tuần, đại lí \(A\) cần \(50\) thùng bánh gạo, đại lí \(B\) cần \(70\) thùng bánh gạo. Chi phí giao hàng cho mỗi thùng bánh gạo của kho ở phía Đông là \(10\) nghìn đồng cho đại lí \(A\) và \(12\) nghìn đồng cho đại lí \(B\). Chi phí giao hàng cho mỗi thùng bánh gạo của kho ở phía Tây là \(9\) nghìn đồng cho đại lí \(A\) và \(11\) nghìn đồng cho đại lí \(B\). Chi phí vận chuyển là nhỏ nhất nhà phân phối cần phải trả là bao nhiêu nghìn đồng?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trả lời: 1295
Gọi \(x,y\) ( \(x \ge 0;y \ge 0\)) lần lượt là số thùng bánh gạo được nhà phân phối chuyển từ kho phía Đông tới hai đại lí \(A\) và \(B.\)
Khi đó \(50 - x;70 - y\)lần lượt là số thùng bánh gạo được nhà phân phối chuyển từ kho phía Tây tới hai đại lí \(A\) và \(B.\)
Ta có hệ bất phương trình
\(\left\{ \begin{array}{l}x + y \le 80\\50 - x + 70 - y \le 45\\0 \le x \le 50\\0 \le y \le 70\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y \le 80\\x + y \ge 75\\0 \le x \le 50\\0 \le y \le 70\end{array} \right.\)
Tổng chi phí giao hàng
\(F\left( {x;y} \right) = 10x + 12y + (50 - x).9 + (70 - y).11{\rm{ }} = {\rm{ }}1220 + x + y{\rm{ }}\)
Miền nghiệm biểu diễn là miền tứ giác \(ABCD\)có \(A\left( {5;70} \right);B\left( {10;70} \right);C\left( {50;30} \right);D\left( {50;25} \right)\)
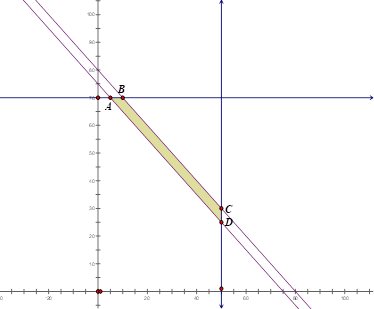
Tính giá trị của \(F\left( {x;y} \right)\) tại các đỉnh \(A,B,C,D\)ta tìm được GTNN là \(F\left( {5;70} \right) = F\left( {50;25} \right) = 1295\).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Các sản phẩm khác của Vietjack:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AM} \).
B. \(\overrightarrow {AG} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\).
C. \(\overrightarrow {AG} = \frac{3}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\).
D. \(\overrightarrow {AG} = \frac{1}{3}\overrightarrow {AM} \).
Lời giải
Đáp án đúng là: B
Ta có \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)\( = \frac{1}{3}\left( {\overrightarrow {AB}+ \overrightarrow {AC} } \right)\).
Lời giải
Trả lời: 5,85
Ta có \(\widehat {ABC} = 180^\circ - 40^\circ - 60^\circ = 80^\circ \).
Theo định lí \(\sin \) trong tam giác \(ABC\), ta có
\(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}} \Rightarrow BC = \frac{{AB.\sin 40^\circ }}{{\sin 60^\circ }} = \frac{{4.\sin 40^\circ }}{{\sin 60^\circ }} \approx 2,97{\rm{cm}}\).
Diện tích tam giác \(ABC\):
\(S = \frac{1}{2}.AB.BC.\sin B = \frac{1}{2}.4.2,97.\sin 80^\circ \approx 5,85{\rm{c}}{{\rm{m}}^{\rm{2}}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\overrightarrow {OA} = \overrightarrow {OC} \).
B. \(\overrightarrow {AB} = \overrightarrow {DC} \).
C. \(\overrightarrow {CB} = \overrightarrow {DA} \).
D. \(\overrightarrow {OB} = \overrightarrow {DO} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập