(1,0 điểm) Cho tứ diện \(ABCD\) và điểm \(M\) thuộc cạnh \(AB\). Gọi \(\left( \alpha \right)\) là mặt phẳng qua \(M\), song song với hai đường thẳng \(BC\) và \(AD\). Gọi \(N,P,Q\) lần lượt là giao điểm của mặt phẳng \(\left( \alpha \right)\) với các cạnh \(AC,CD\) và \(DB\).
a) Chứng minh \(MNPQ\) là hình bình hành.
b) Trong trường hợp nào thì \(MNPQ\) là hình thoi?
(1,0 điểm) Cho tứ diện \(ABCD\) và điểm \(M\) thuộc cạnh \(AB\). Gọi \(\left( \alpha \right)\) là mặt phẳng qua \(M\), song song với hai đường thẳng \(BC\) và \(AD\). Gọi \(N,P,Q\) lần lượt là giao điểm của mặt phẳng \(\left( \alpha \right)\) với các cạnh \(AC,CD\) và \(DB\).
a) Chứng minh \(MNPQ\) là hình bình hành.
b) Trong trường hợp nào thì \(MNPQ\) là hình thoi?
Câu hỏi trong đề: Bộ 10 đề thi Giữa kì 1 Toán 10 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
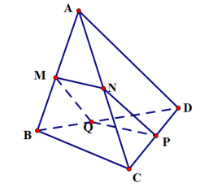
a) \(\left( \alpha \right)\,{\rm{//}}\,BC,BC \subset \left( {ABC} \right)\) và \(\left( \alpha \right)\) cắt \(\left( {ABC} \right)\) tại \(MN\) nên \(MN\,{\rm{//}}\,BC\).
\(\left( \alpha \right)\,{\rm{//}}\,BC,BC \subset \left( {BCD} \right)\) và \(\left( \alpha \right)\) cắt \(\left( {BCD} \right)\) tại \(PQ\) nên \(PQ\,{\rm{//}}\,BC\).
Suy ra: \(MN\,{\rm{//}}\,PQ\).
\(\left( \alpha \right)\,{\rm{//}}\,AD,AD \subset \left( {ABD} \right)\) và \(\left( \alpha \right)\) cắt \(\left( {ABD} \right)\) tại \(MQ\) nên \(MQ\,{\rm{//}}\,AD\).
\(\left( \alpha \right)\,{\rm{//}}\,AD,AD \subset \left( {ACD} \right)\) và \(\left( \alpha \right)\) cá́t \(\left( {ACD} \right)\) tại \(NP\) nên \(NP\,{\rm{//}}\,BC\).
Suy ra: \(MQ\,{\rm{//}}\,NP\).
Do đó, \(MNPQ\) là hình bình hành.
b) \(MNPQ\) là hình thoi khi \(MN = NP\).
Ta có: \(\frac{{MN}}{{BC}} = \frac{{AN}}{{AC}}\)
\(\frac{{NP}}{{AD}} = \frac{{CN}}{{AC}}\) hay \({\rm{\;}}\frac{{MN}}{{AD}} = \frac{{CN}}{{AC}}\)
Mà \(\frac{{AN}}{{AC}} + \frac{{CN}}{{AC}} = 1\) nên \(\frac{{MN}}{{BC}} + \frac{{MN}}{{AD}} = 1\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x,\,y\) lần lượt là số radio kiểu một và kiểu hai sản xuất được trong một ngày. \(\left( {x,\,\,y \ge 0} \right)\)
Vì radio kiểu một sản xuất trên dây chuyền một với công suất 45 radio/ngày, radio kiểu hai sản xuất trên dây chuyền hai với công suất 80 radio/ngày nên \(x \le 45,\,\,y \le 80\).
Sản xuất \(x\) chiếc radio kiểu một và \(y\) chiếc radio kiểu hai cần số linh kiện là \(12x + 9y\).
Mà số linh kiện có thể sử dụng tối đa trong một ngày là 900 nên \(12x + 9y \le 900\) hay tương đương với \(4x + 3y \le 300\).
Tiền lãi thu được khi bán \(x\) chiếc radio kiểu một và \(y\) chiếc radio kiểu hai là \(T = 250\,\,000x + 180\,\,000y\) (đồng).
Khi đó, bài toán đã cho trở thành: Tìm \(\left( {x;\,\,y} \right)\) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}0 \le x \le 45\\0 \le y \le 80\\4x + 3y \le 300\end{array} \right.\)để \(T = 250\,\,000x + 180\,\,000y\) lớn nhất.
Biểu diễn miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}0 \le x \le 45\\0 \le y \le 80\\4x + 3y \le 300\end{array} \right.\) lên mặt phẳng tọa độ \(Oxy\) ta được:
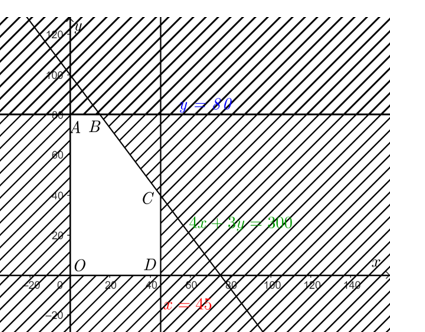
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}0 \le x \le 45\\0 \le y \le 80\\4x + 3y \le 300\end{array} \right.\) là miền ngũ giác \(OABCD\) (kể cả biên) với \(O\left( {0;\,\,0} \right),\,\,A\left( {0;\,\,80} \right),\,\,B\left( {15;\,\,80} \right),\,\,C\left( {45;\,\,40} \right),\,\,D\left( {45;\,\,0} \right)\).
Người ta chứng minh được \(T = 250\,\,000x + 180\,\,000y\) đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác \(OABCD\).
Ta có: \(T\left( {0;\,\,0} \right) = 0\);
\(T\left( {0;\,\,80} \right) = 250\,\,000 \cdot 0 + 180\,\,000 \cdot 80 = 14\,\,400\,\,000\);
\(T\left( {15;\,\,80} \right) = 250\,\,000 \cdot 15 + 180\,\,000 \cdot 80 = 18\,\,150\,\,000\);
\(T\left( {45;\,\,40} \right) = 250\,\,000 \cdot 45 + 180\,\,000 \cdot 40 = 18\,\,450\,\,000\);
\(T\left( {45;\,\,0} \right) = 250\,\,000 \cdot 45 + 180\,\,000 \cdot 0 = 11\,\,250\,\,000\).
Do đó, \(T = 250\,\,000x + 180\,\,000y\) đạt giá trị lớn nhất tại \(\left( {x;\,\,y} \right) = \left( {45;\,\,40} \right)\).
Vậy cần sản xuất 45 radio kiểu một và 40 radio kiểu hai thì lãi thu được trong một ngày là lớn nhất.
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Diện tích tam giác \[ABC\] đều là:
\[S = AB.AC.sinA = \frac{1}{2}.2a.2a.sin60^\circ = {a^2}\sqrt 3 \]
Nửa chu vi tam giác \[ABC\] là:
\[p = \frac{{2a + 2a + 2a}}{2} = 3a\]
Bán kính đường tròn nội tiếp tam giác \[ABC\] là:
\[r = \frac{S}{p} = \frac{{{a^2}\sqrt 3 }}{{3a}} = \frac{a}{{\sqrt 3 }}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.