Một cửa hàng nhân dịp Noel đã đồng loạt giảm giá các sản phẩm. Trong đó có chương trình nếu mua một gói kẹo thứ hai trở đi sẽ được giảm \(10\% \) so với giá ban đầu. Biết giá gói đầu là 60000 đồng. Bạn An có 500000 đồng. Hỏi bạn An có thể mua tối đa bao nhiêu gói kẹo?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trả lời: 9
Xét một người mua \(x\) gói kẹo ( \(x\) nguyên dương).
Khi đó: Gói thứ nhất người đó trả 60000 đồng.
Số gói kẹo còn lại là \(x - 1\) và người đó chỉ phải trả
\(60000 - 10\% .60000 = 54000\) đồng (mỗi gói).
Vậy số tiền phải trả khi mua kẹo được tính theo công thức
\(y = 60000 + (x - 1) \cdot 54000 = 54000x + 6000\).
Số tiền bạn An dùng mua kẹo phải không quá 500000 đồng, suy ra: \(54000x + 6000 \le 500000 \Rightarrow x \le \frac{{247}}{{27}} \approx 9,148\).
Vậy, với số tiền hiện có, bạn An chỉ có thể mua được tối đa 9 gói kẹo.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Trả lời: 0
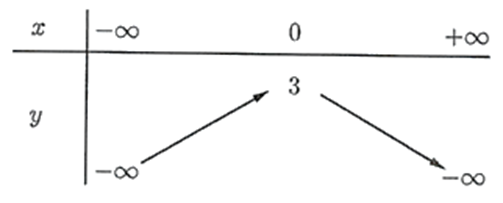
Ta có điêu kiện: \( - 20 < x < 30\).
Diện tích hình chữ nhật lúc sau là: \(S = (30 - x) \cdot (20 + x) = - {x^2} + 10x + 600\;{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Diện tích hình chữ nhật lúc đầu là \(600\;{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Đặt \(f(x) = - {x^2} + 10x + 600 - 600 = - {x^2} + 10x\).
\(f(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 10}\end{array}} \right.\).
Ta có bảng xét dấu của \(f(x)\)
Diện tích của khung sau khi uốn tăng lên khi \(f(x) > 0 \Leftrightarrow x \in (0;10)\).
Suy ra \(a = 0;b = 10\). Do đó \(a.b = 0\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Đ, b) S, c) S, d) Đ
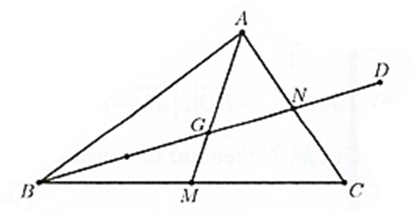
a) \(\overrightarrow {MD} = \overrightarrow {MG} + \overrightarrow {GD} \).
b) Ta có: \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} = \frac{2}{3} \cdot \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} ) = \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
c) Ta có: \(\overrightarrow {CD} = \overrightarrow {CB} + \overrightarrow {BD} = \overrightarrow {AB} - \overrightarrow {AC} + \frac{4}{3}\overrightarrow {BN} \).
d) Ta có: \(\overrightarrow {MD} = \overrightarrow {MG} + \overrightarrow {GD} = - \frac{1}{3}\overrightarrow {AM} + \frac{2}{3}\overrightarrow {BN} = - \frac{1}{3} \cdot \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} ) + \frac{2}{3}(\overrightarrow {BA} + \overrightarrow {AN} )\)
\( = - \frac{1}{6}\overrightarrow {AB} - \frac{1}{6}\overrightarrow {AC} - \frac{2}{3}\overrightarrow {AB} + \frac{2}{3} \cdot \frac{1}{2}\overrightarrow {AC} = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} {\rm{. }}\)
Câu 3
A. \(b = - 1\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(6\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập