(1 điểm) Cho tam giác \[ABC\] có trực tâm \(H\). Gọi \(M\) là trung điểm của cạnh \(BC\). Chứng minh rằng \[\overrightarrow {MH} \cdot \overrightarrow {MA} = \frac{1}{4}B{C^2}\].

Đáp án đúng là: A

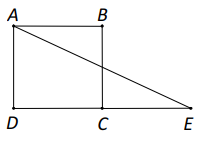
Vì \(E\) là điểm đối xứng của \(D\) qua \(C\) nên \(C\) là trung điểm của \(DE\), do đó \(DE = 2DC = 2 \cdot 3 = 6\).

Ta có: \(\overrightarrow {AE} \cdot \overrightarrow {AB} = \left( {\overrightarrow {AD} + \overrightarrow {DE} } \right) \cdot \overrightarrow {AB} = \overrightarrow {AD} \cdot \overrightarrow {AB} + \overrightarrow {DE} \cdot \overrightarrow {AB} \)

Do \(AB \bot AD\) nên \(\overrightarrow {AD} \cdot \overrightarrow {AB} = 0\).

Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DE} \) cùng hướng nên \(\cos \left( {\overrightarrow {AB} ,\,\,\overrightarrow {DE} } \right) = 0^\circ \).

Do đó, \(\overrightarrow {DE} \cdot \overrightarrow {AB} = \left| {\overrightarrow {DE} } \right| \cdot \left| {\overrightarrow {AB} } \right| \cdot \cos \left( {\overrightarrow {AB} ,\,\overrightarrow {DE} } \right) = DE \cdot AB \cdot \cos 0^\circ = 6 \cdot 3 \cdot 1 = 18\).

Vậy \(\overrightarrow {AE} \cdot \overrightarrow {AB} = 0 + 18 = 18\).

Gọi \(x,\,y\) lần lượt là số block công ty đó thuê quảng cáo trên đài phát thanh và trên đài truyền hình.

Chi phí công ty cần bỏ ra là \(10x + 25y\) (triệu đồng). Mức chi này không vượt quá chi phí công ty đặt ra nên \(10x + 25y \le 500\) hay \(2x + 5y \le 100\).

Do các điều kiện đài phát thanh và đài truyền hình đưa ra nên ta có \(x \ge 5;\,y \ge 10\).

Hiệu quả quảng cáo (phần trăm tăng tưởng sản phẩm do quảng cáo) là \(F\left( {x;\,\,y} \right) = 0,02x + 0,04y\).

Bài toán trở thành: Xác định \(x,\,\,y\) sao cho \(F\left( {x;\,\,y} \right)\) đạt giá trị lớn nhất với các điều kiện \(\left\{ \begin{array}{l}2x + 5y \le 100\\x \ge 5\\y \ge 10\end{array} \right.\) (*).

Biểu diễn miền nghiệm của hệ bất phương trình (*) lên mặt phẳng tọa độ \(Oxy\) ta được:

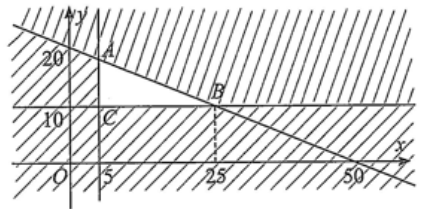
Miền nghiệm của hệ (*) là miền tam giác \(ABC\) với \(A\left( {5;\,\,18} \right),\,\,B\left( {25;\,\,10} \right),\,\,C\left( {5;\,\,10} \right)\).

Ta có: \(F\left( {5;\,\,18} \right) = 0,02 \cdot 5 + 0,04 \cdot 18 = 0,82\);

\(F\left( {25;\,\,10} \right) = 0,02 \cdot 25 + 0,04 \cdot 10 = 0,9\);

\(F\left( {5;\,\,10} \right) = 0,02 \cdot 5 + 0,04 \cdot 10 = 0,5\).

Do đó, giá trị lớn nhất của \(F\left( {x;\,\,y} \right)\) bằng 0,9 tại \(\left( {x;\,y} \right) = \left( {25;\,\,10} \right)\).

Vậy để đạt hiệu quả cao nhất thì công ty đó cần quảng cáo 25 block trên đài phát thanh và 10 block trên đài truyền hình.