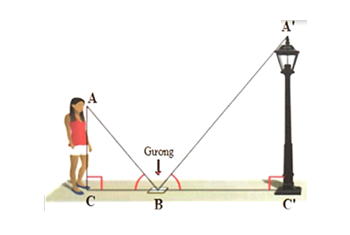
Để đo chiều cao của một cột đèn ta làm như sau: Đặt tấm gương phẳng nằm trên mặt phẳng nằm ngang, mắt của người quan sát nhìn thẳng vào gương, người quan sát di chuyển sao cho thấy được đỉnh ngọn đèn trong tấm gương và \(\widehat {ABC} = \widehat {A'BC'}.\) Cho chiều cao tính từ mắt của người quan sát đến mặt đất là \(AC = 1,5\;\,{\rm{m;}}\) khoảng cách từ gương đến chân người là \(BC = 0,75\;\,{\rm{m;}}\) khoảng cách từ gương đến chân cột đèn là \(BC' = 1,4\;{\rm{m}}{\rm{.}}\) Hỏi chiều cao của cột đèn là bao nhiêu mét? (Kết quả ghi dưới dạng số thập phân)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: 2,8
\(\Delta BCA\) và \(\Delta BC'A'\) có: \(\widehat {ACB} = \widehat {BC'A'} = 90^\circ ;\;\,\widehat {ABC} = \widehat {A'BC'}\) nên \(\Delta BCA \sim \Delta BC'A'\) (g.g).
Do đó, \(\frac{{BC}}{{BC'}} = \frac{{AC}}{{A'C'}}\) suy ra \(A'C' = \frac{{AC \cdot BC'}}{{BC}} = \frac{{1,5 \cdot 1,4}}{{0,75}} = 2,8\;\,\left( {\rm{m}} \right).\)
Vậy chiều cao cột đèn bằng \(2,8\;\,{\rm{m}}{\rm{.}}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
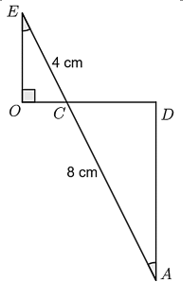
Câu 1
b) \(A{H^2} = AN \cdot AC.\)
b) \(A{H^2} = AN \cdot AC.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
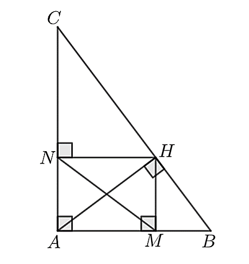
a) Đúng.
Vì \(M,\;\,N\) lần lượt là hình chiếu của \(H\) trên \(AB,\;\,AC\) nên \(HM \bot AB;\;\,HN \bot AC.\)
Do đó, \(\widehat {AMH} = \widehat {HMB} = \widehat {ANH} = \widehat {HNC} = 90^\circ .\)
Vì \(AH\) là đường cao của tam giác \(ABC\) nên \(AH \bot BC.\) Suy ra \(\widehat {AHB} = \widehat {AHC} = 90^\circ .\)
\(\Delta AHM\) và \(\Delta ABH\) có: \(\widehat {AMH} = \widehat {AHB} = 90^\circ ;\;\,\widehat {HAM}\) chung nên \(\Delta AHM \sim \Delta ABH\) (g.g).
b) Đúng.
\(\Delta AHN\) và \(\Delta ACH\) có: \(\widehat {ANH} = \widehat {AHC} = 90^\circ ;\;\,\widehat {HAN}\) chung nên \(\Delta AHN \sim \Delta ACH\) (g.g).
Do đó, \(\frac{{AH}}{{AC}} = \frac{{AN}}{{AH}}.\) Suy ra \(A{H^2} = AN \cdot AC.\)
c) Sai.
Theo a) ta có: \(\Delta AHM \sim \Delta ABH\) (g.g) nên \(\frac{{AM}}{{AH}} = \frac{{AH}}{{AB}}.\) Suy ra \(AM \cdot AB = A{H^2}.\)
Mà \(A{H^2} = AN \cdot AC\) nên \(AM \cdot AB = AN \cdot AC.\)
d) Đúng.
Vì \(AM \cdot AB = AN \cdot AC\) nên \(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}.\)
\(\Delta ANM\) và \(\Delta ABC\) có: \(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}};\;\,\widehat {NAM} = \widehat {BAC} = 90^\circ \) chung nên \(\Delta ANM \sim \Delta ABC\)(c.g.c).
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: A
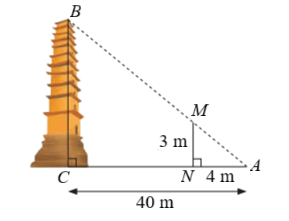
Nhận thấy \(\Delta ABC\) và \(\Delta DEC\) có \(\widehat {BAC} = \widehat {EDC} = 90^\circ \) và \(\widehat {ACB} = \widehat {ECD}\) (góc chung).
Do đó, \(\Delta ABC \sim \Delta DEC\) (g.g)
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập