(1 điểm) Cho tam giác đều \(ABC\) cạnh \(a\). Xác định tập hợp các điểm \(M\) thỏa mãn đẳng thức \[4M{A^2} + M{B^2} + M{C^2} = \frac{{5{a^2}}}{2}\].
(1 điểm) Cho tam giác đều \(ABC\) cạnh \(a\). Xác định tập hợp các điểm \(M\) thỏa mãn đẳng thức \[4M{A^2} + M{B^2} + M{C^2} = \frac{{5{a^2}}}{2}\].
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 10 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Gọi \(N\) là trung điểm của \(BC\).
Gọi \(I\) là điểm thỏa mãn điều kiện: \[4\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \].
Khi đó, ta có: \[4\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \]\[ \Leftrightarrow 4\overrightarrow {IA} + 2\overrightarrow {IN} = \overrightarrow 0 \Leftrightarrow 2\overrightarrow {IA} + \overrightarrow {IN} = \overrightarrow 0 \], do đó điểm \(I\) thuộc đoạn \(AN\) sao cho \(IN = 2IA\).
![(1 điểm) Cho tam giác đều \(ABC\) cạnh \(a\). Xác định tập hợp các điểm \(M\) thỏa mãn đẳng thức \[4M{A^2} + M{B^2} + M{C^2} = \frac{{5{a^2}}}{2}\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/21-1763471407.png)
Lại có tam giác \(ABC\) đều cạnh \(a\) nên \(AN = \frac{{a\sqrt 3 }}{2}\).
Suy ra: \[IA = \frac{1}{2}AN = \frac{1}{3} \cdot \frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}\]; \(IN = \frac{2}{3}AN = \frac{2}{3} \cdot \frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\) ;
\[IB = IC = \sqrt {I{N^2} + B{N^2}} = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt {21} }}{6}\].
Ta lại có: \[4M{A^2} + M{B^2} + M{C^2} = \frac{{5{a^2}}}{2}\]
\[ \Leftrightarrow 4{\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2} + {\overrightarrow {MC} ^2} = \frac{{5{a^2}}}{2}\]
\[ \Leftrightarrow 4{\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {IC} } \right)^2} = \frac{{5{a^2}}}{2}\]
\[ \Leftrightarrow 6M{I^2} + 2\overrightarrow {MI} \left( {4\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} } \right) + 4I{A^2} + I{B^2} + I{C^2} = \frac{{5{a^2}}}{2}\]
\( \Leftrightarrow 6M{I^2} + 4 \cdot {\left( {\frac{{a\sqrt 3 }}{6}} \right)^2} + {\left( {\frac{{a\sqrt {21} }}{6}} \right)^2} + {\left( {\frac{{a\sqrt {21} }}{6}} \right)^2} = \frac{{5{a^2}}}{2}\)
\[ \Leftrightarrow MI = \frac{a}{{\sqrt 6 }}\].
Vậy tập hợp điểm \(M\) là đường tròn tâm \(I\) bán kính \[R = \frac{a}{{\sqrt 6 }}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
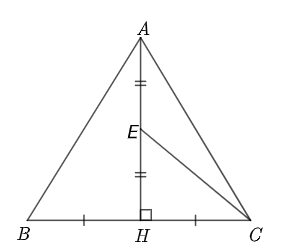
Ta có: \[\left| {\overrightarrow {CA} + \overrightarrow {CH} } \right| = \left| {2\overrightarrow {CE} } \right| = 2CE\] (với \[E\] là trung điểm của \[AH\]).
Ta lại có: \[AH = \frac{{5\sqrt 3 }}{2}\] (\[\Delta ABC\] đều, \[AH\] là đường cao), suy ra \(HE = \frac{1}{2}AH = \frac{{5\sqrt 3 }}{4}\).
\(CH = \frac{1}{2}BC = \frac{5}{2}\).
Trong tam giác \[HEC\] vuông tại \[H\], từ định lí Pythagore suy ra
\[EC = \sqrt {C{H^2} + H{E^2}} = \sqrt {{{\left( {\frac{5}{2}} \right)}^2} + {{\left( {\frac{{5\sqrt 3 }}{4}} \right)}^2}} = \frac{{5\sqrt 7 }}{4}\]
\[ \Rightarrow \left| {\overrightarrow {CA} - \overrightarrow {HC} } \right| = 2CE = \frac{{5\sqrt 7 }}{2}\].
Câu 2
Số nhân khẩu trong các hộ gia đình ở một xóm được thống kê ở bảng sau:
|
Số nhân khẩu |
1 |
2 |
3 |
4 |
5 |
|
Số hộ gia đình |
1 |
5 |
6 |
9 |
7 |
Mốt của mẫu số liệu trên là
Lời giải
Đáp án đúng là: D
Từ bảng số liệu ta thấy giá trị 4 có tần số lớn nhất (9) nên mốt của mẫu số liệu là 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.