Một cây cột điện cao \[20{\rm{ }}m\] được đóng trên một triền dốc thẳng nghiêng hợp với phương nằm ngang một góc \[17^\circ \]. Người ta nối một dây cáp từ đỉnh cột điện đến cuối dốc.

 

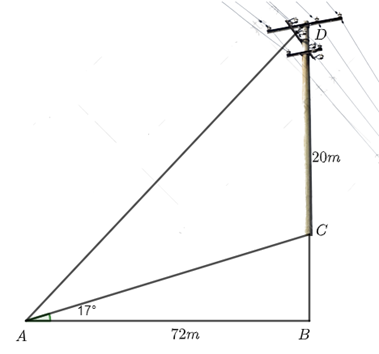
Chiều dài của dây cáp bằng bao nhiêu? (Biết rằng đoạn đường từ đáy cọc đến cuối dốc bằng \[72{\rm{ }}m\]).

Hướng dẫn giải

Gọi hàm quỹ đạo parabol của quả bóng là \(h\left( t \right) = a{t^2} + bt + c\left( {a \ne 0} \right)\).

Quả bóng được đá lên từ độ cao \(1,2m\) nên \(t = 0\), ta có điểm \(\left( {0;\,\,1,2} \right)\), thay \(t = 0\) và \(h = 1,2\) vào hàm số trên ta được: \(c = 1,2\).

\( \Rightarrow h\left( t \right) = a{t^2} + bt + 1,2\) \(\left( 1 \right)\)

Tại \(t = 1\) thì \(h = 8,5\) khi đó \(\left( 1 \right) \Leftrightarrow a + b + 1,2 = 8,5 \Leftrightarrow a + b = 7,3\) \(\left( 2 \right)\).

Tại \(t = 2\) thì \(h = 6\) khi đó \(\left( 1 \right) \Leftrightarrow 4a + 2b + 1,2 = 6 \Leftrightarrow 4a + 2b = 4,8 \Leftrightarrow 2a + b = 2,4\) \(\left( 3 \right)\).

Từ \(\left( 2 \right)\) và \(\left( 3 \right)\) ta có hệ phương trình: \(\left\{ \begin{array}{l}a + b = 7,3\\2a + b = 2,4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 4,9\\b = 12,2\end{array} \right.\)(thỏa mãn điều kiện).

Do đó hàm số cần tìm là \(h\left( t \right) = - 4,9{t^2} + 12,2t + 1,2\).

Quả bóng chạm đất nghĩa là độ cao bằng \(0\) khi đó \(h = 0\), thay vào hàm số trên ta được:

\( - 4,9{t^2} + 12,2t + 1,2 = 0 \Leftrightarrow \left[ \begin{array}{l}t \approx 2,58\\t \approx - 0,09\end{array} \right.\).

Vì \(t > 0\) nên \(t \approx 2,58\) thỏa mãn.

Vậy sau khoảng \(2,58\) giây thì quả bóng chạm đất.