Trong các khẳng định sau, khẳng định nào đúng?
Trong các khẳng định sau, khẳng định nào đúng?
Quảng cáo
Trả lời:
Chọn A
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn D
![Cho tứ diện \[ABC{\rm{D}}\] có \[M,N\] lần lượt là trung điểm của \[AB,AC\]. Mặt phẳng nào sau đây song song với đường thẳng \[MN\]? A. \[(ACD)\]. B. \[(ABD)\] C. \[(ABC)\] D. \[(BCD)\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/15-1764167913.png)
\(\left\{ \begin{array}{l}MN//\,BC\\BC \subset \left( {BCD} \right)\end{array} \right. \Rightarrow MN//\left( {BCD} \right)\)
Lời giải
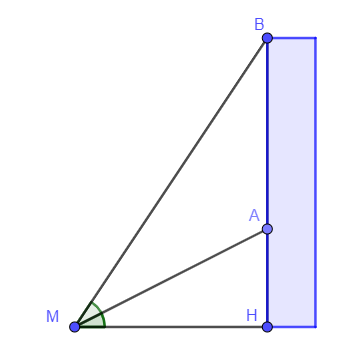
\[\widehat {AMH} = x\,\,\left( {0 < x < 90^\circ } \right) \Rightarrow \widehat {BMH} = 2x\]
\[\tan 2x = \frac{{2\tan x}}{{1 - {{\tan }^2}x}} = \frac{{BH}}{{MH}} = \frac{{3AH}}{{MH}} = 3\tan x\]
\[\tan x = \frac{1}{{\sqrt 3 }} \Rightarrow x = 30^\circ \]
(HS tính ra góc \[\frac{\pi }{6}\] rad được chấp nhận)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.