Tập xác định của hàm số \(y = \cot x\) là

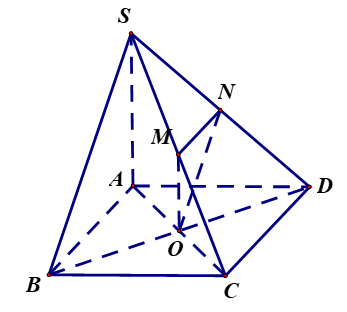
a) Do \(ABCD\) là hình bình hành nên \(CD\,{\rm{//}}\,AB\).

Ta có: \(\left\{ \begin{array}{l}CD\,{\rm{//}}\,AB\\CD\, \not\subset \,\,(\,SAB\,)\,\,\\AB\, \subset \,(SAB\,)\end{array} \right.\, \Rightarrow \,CD\,{\rm{//}}\,(\,SAB)\) (điều phải chứng minh).

b) Ta có \(OM,MN\) là đường trung bình của tam giác \(SAC\) và tam giác \(SBD\)

\(\left\{ \begin{array}{l}OM||SA\\OM \not\subset \left( {SAB} \right)\\SA \subset \left( {SAB} \right)\end{array} \right. \Rightarrow OM//\left( {SAB} \right)\)(1)

\(\left\{ \begin{array}{l}ON||SB\\ON \not\subset \left( {SAB} \right)\\SB \subset \left( {SAB} \right)\end{array} \right. \Rightarrow ON//\left( {SAB} \right)\) (2)

Từ (1), (2) và \(ON \cap OM = O,OM,ON \subset \left( {OMN} \right) \Rightarrow \left( {OMN} \right)//\left( {SAB} \right)\)

c) Gọi \((P)\) là mặt phẳng đi qua điểm \(O\) và song song với mặt phẳng \(\left( {SBC} \right)\). Xác định giao tuyến của mặt phẳng \((P)\)với các mặt phẳng \[(ABCD)\]và \[(SAB)\].

Ta có \[\left\{ \begin{array}{l}O \in \left( P \right) \cap \left( {ABCD} \right)\\\left( P \right)//\left( {SBC} \right)\\\left( {ABCD} \right) \cap \left( {SBC} \right) = BC\end{array} \right. \Rightarrow \left( P \right) \cap \left( {ABCD} \right) = Ox,Ox//BC\]

Gọi \(Ox \cap AB = Q\)

\[\left\{ \begin{array}{l}Q \in \left( P \right) \cap \left( {SAB} \right)\\\left( P \right)//\left( {SBC} \right)\\\left( {SAB} \right) \cap \left( {SBC} \right) = SB\end{array} \right. \Rightarrow \left( P \right) \cap \left( {SAB} \right) = Qy,Oy//SB\].

d)

Cách 1:

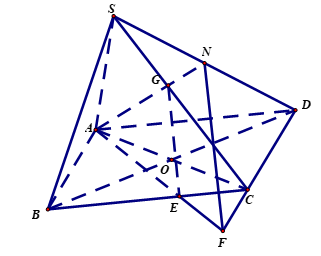
Gọi \(F\) là giao điểm của \(AE\) và \(CD\) trong mặt phẳng \(\left( {ABCD} \right)\).

Ta có: \(\left\{ \begin{array}{l}GE \subset \left( {ANF} \right)\\GE//\left( {SCD} \right)\\\left( {ANF} \right) \cap \left( {SCD} \right) = NF\end{array} \right. \Rightarrow GE//NF\)

\( \Rightarrow \frac{{FE}}{{FA}} = \frac{{NG}}{{NA}} = \frac{1}{3}\)

Theo Talet, ta có: \(\frac{{EC}}{{AD}} = \frac{{FE}}{{FA}} = \frac{1}{3}\)\( \Rightarrow EC = \frac{1}{3}AD = \frac{1}{3}BC \Rightarrow \frac{{EB}}{{EC}} = 2\)

Nhận xét: \(\Delta EAB\) và \(\Delta EAC\) có chung đường cao kẻ từ \(A\).

Do đó: \(\frac{{{S_{\Delta EAB}}}}{{{S_{\Delta EAC}}}} = \frac{{EB}}{{EC}} = 2\).

Cách 2:

Vẽ \(GF\) song song với \(SD\)\(\left( {F \in AD} \right)\).

Ta chứng minh được: \(\left( {GEF} \right)//\left( {SCD} \right) \Rightarrow EF//CD\)

Từ đó suy ra được:

\(\frac{{EC}}{{BC}} = \frac{{FD}}{{AD}} = \frac{{GN}}{{AN}} = \frac{1}{3} \Rightarrow EC = \frac{1}{3}BC\)

Nhận xét: \(\Delta EAB\) và \(\Delta EAC\) có chung đường cao kẻ từ \(A\)

 Do đó: \(\frac{{{S_{\Delta EAB}}}}{{{S_{\Delta EAC}}}} = \frac{{EB}}{{EC}} = 2\)

Gọi \[x\] là số tiền bác An gửi ngân hàng \[MSB\].

\[320000000 - x\] là số tiền bác An gửi ngân hàng VietinBank.

Sau 15 tháng số tiền lãi ở ngân hàng \[MSB\] là \[x{(1 + 2,1\% )^5} - x\].

Sau 9 tháng số tiền lãi ở ngân hàng VietinBank là \[(320000000 - x){(1 + 0.73\% )^9} - (320000000 - x)\].

Ta có \[x{(1 + 2,1\% )^5} - x + (320000000 - x){(1 + 0,73\% )^9} - (320000000 - x) = 26670725,95\].

\[ \Leftrightarrow x = 120000000\].

Vậy số tiền bác An gửi vào hai ngân hàng\[MSB\]là \(120\) triệu đồng và ngân hàng VietinBank \(200\) triệu đồng