Cho bất phương trình \({\left( {\frac{1}{6}} \right)^{x + 2}} \le {\left( {\frac{1}{{36}}} \right)^{ - x}}\), có tập nghiệm là \(S = \left[ {a;b} \right)\). Khi đó:

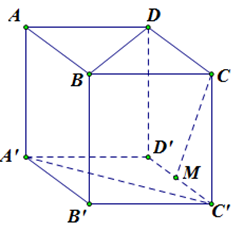
Ta có \(AA'\,{\rm{// }}\left( {DD'C'C} \right) \supset CM\)\( \Rightarrow d\left( {AA',CM} \right) = d\left( {AA',\left( {DD'C'C} \right)} \right) = AD = a\).

Trả lời: \( \approx {25,7^0}\)

Lời giải

Kẻ \({C^\prime }I \bot {A^\prime }{B^\prime }\)

Ta có: \({C^\prime }I \bot {A^\prime }A \Rightarrow {C^\prime }I \bot \left( {A{A^\prime }{B^\prime }B} \right)\) tại \(I\) và \({C^\prime }A\) cắt mp\(\left( {A{A^\prime }{B^\prime }B} \right)\) tại \(A\).

\( \Rightarrow AI\) là hình chiếu của \({C^\prime }A\) trên mp\(\left( {A{A^\prime }{B^\prime }B} \right)\)

\( \Rightarrow \left( {{C^\prime }A,\left( {A{A^\prime }{B^\prime }B} \right)} \right) = \left( {{C^\prime }A,AI} \right) = \widehat {{C^\prime }AI}\)

Ta có: \({A^\prime }A = AB \cdot \tan {60^^\circ } = \sqrt 3 a\)

\(AI = \sqrt {{A^\prime }{A^2} + {A^\prime }{I^2}}  = \sqrt {{{(a\sqrt 3 )}^2} + {{\left( {\frac{a}{2}} \right)}^2}}  = \frac{{\sqrt {13} }}{2}a\)

Xét \(\Delta {C^\prime }AI\) vuông tại \(I:\tan \widehat {{C^\prime }AI} = \frac{{{C^\prime }I}}{{AI}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{\frac{{\sqrt {13} a}}{2}}} = \frac{{\sqrt {39} }}{{13}} \Rightarrow \widehat {{C^\prime }AI} \approx {25,7^0}\)