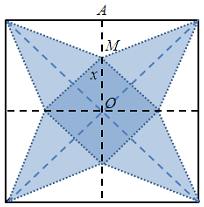
Cắt một miếng giấy hình vuông như hình bên và xếp thành hình một hình chóp tứ giác đều. Biết các cạnh hình vuông bằng \(20\)cm, \(OM = x\)(cm). Tìm \(x\) để hình chóp đều ấy có thể tích lớn nhất (đơn vị: cm)

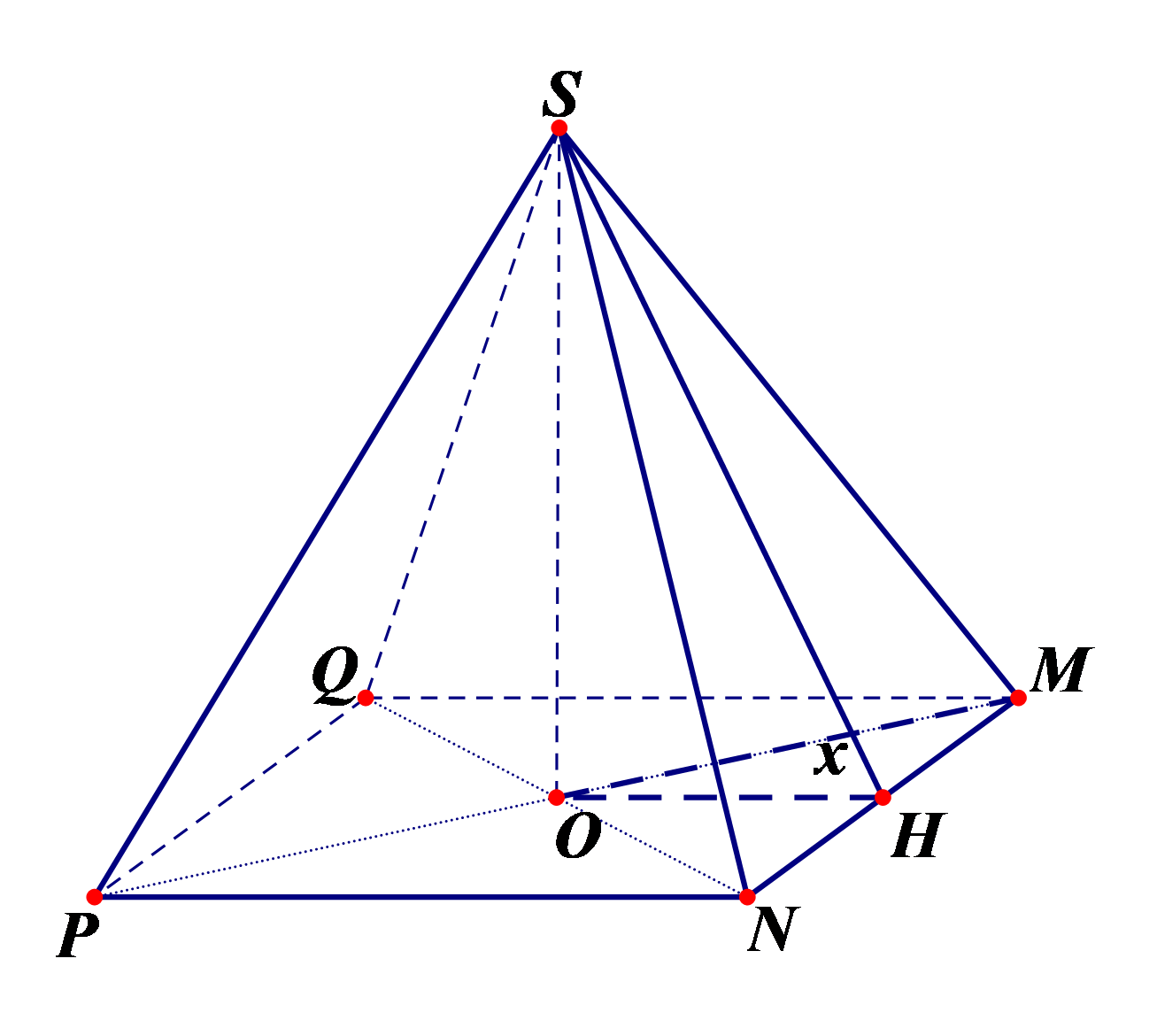
Giả sử được hình chóp tứ giác đều như hình vẽ có cạnh đáy bằng \(x\sqrt 2 \).

Khi đó: \(OM = x\) \( \Rightarrow OH = HM = \frac{x}{{\sqrt 2 }}\) \( \Rightarrow SH = 10\sqrt 2  - \frac{x}{{\sqrt 2 }}\).

Suy ra: \[SO = \sqrt {S{H^2} - O{H^2}}  = \sqrt {{{\left( {10\sqrt 2  - \frac{x}{{\sqrt 2 }}} \right)}^2} - {{\left( {\frac{x}{{\sqrt 2 }}} \right)}^2}}  = \sqrt {20\left( {10 - x} \right)} \].

Thể tích \(V = \frac{1}{3}.{S_{MNPQ}}.SO\) \( = \frac{1}{3}.2{x^2}.\sqrt {20\left( {10 - x} \right)} \) \( = \frac{{\sqrt {20} }}{3}.{x^2}.\sqrt {40 - 4x} \) (với \(0 \le x \le 10\)).

Tìm giá trị lớn nhất của \(V\) ta được \({V_{\max }} = \frac{{\sqrt {20} }}{3}{.10^2}\) khi \(x = 8\).

Có thể tìm giá trị lớn nhất bằng cách áp dụng BĐT Cauchy cho 4 số không âm, ta có:

\({x^2}.\sqrt {40 - 4x}  = \sqrt {\left( {40 - 4x} \right).x.x.x.x} . \le {\left( {\sqrt {\frac{{40 - 4x + x + x + x + x}}{4}} } \right)^4}\)\( \Leftrightarrow \sqrt {40 - 4x} .{x^2} \le {10^2}\).

Vậy\(V = \frac{{\sqrt {20} }}{3}.{x^2}\sqrt {40 - 4x}  \le \frac{{\sqrt {20} }}{3}{.10^2}\). Dấu bằng xảy ra khi \(40 - 4x = x \Leftrightarrow x = 8\).