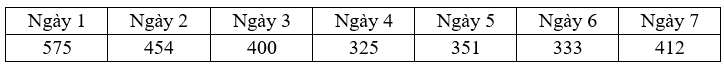Một nhà vòm chứa máy bay có mặt cắt hình nửa elip cao 5 m, rộng 20 m. Khoảng cách theo phương thẳng đứng từ một điểm cách chân tường 5 m lên đến nóc nhà vòm bằng \(\frac{{a\sqrt b }}{c}\) với \(a,\,b,\,c\) là các số nguyên dương. Tính giá trị biểu thức \(T = a + 2b - c\).
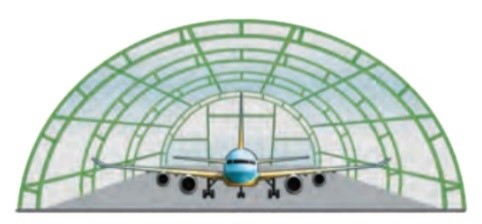
Một nhà vòm chứa máy bay có mặt cắt hình nửa elip cao 5 m, rộng 20 m. Khoảng cách theo phương thẳng đứng từ một điểm cách chân tường 5 m lên đến nóc nhà vòm bằng \(\frac{{a\sqrt b }}{c}\) với \(a,\,b,\,c\) là các số nguyên dương. Tính giá trị biểu thức \(T = a + 2b - c\).

Quảng cáo
Trả lời:
Chọn hệ trục tọa độ \[Oxy\] với gốc tọa độ tại tâm đáy nhà vòm, trục tung thẳng đứng.
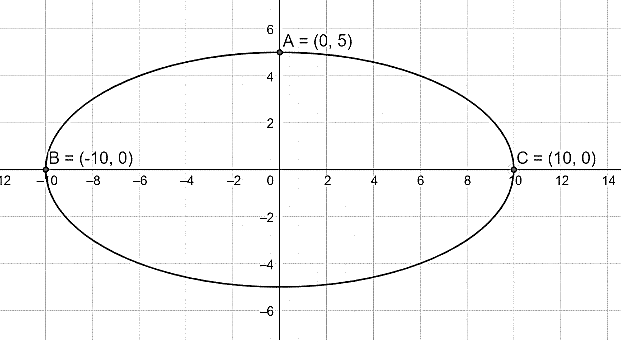
Nhà vòm có dạng nửa elip nên có phương trình chính tắc của elip là \[\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\] (\[a,\,b > 0\]).
Ta có chiều cao của nhà vòm là 5m nên \[OA = h = 5\], chiều rộng của nhà vòm là 20m nên\[BC = 2OB = 20\]. Suy ra \[OB = 10\].
Ta có tọa độ các điểm: \[C\left( {10;\,0} \right)\] và \[A\left( {0;\,5} \right)\]. Thay hai điểm này vào phương trình chính tắc, ta có
\[\left\{ \begin{array}{l}\frac{{{{10}^2}}}{{{a^2}}} + \frac{{{0^2}}}{{{b^2}}} = 1\\\frac{{{0^2}}}{{{a^2}}} + \frac{{{5^2}}}{{{b^2}}} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 10\\b = 5.\end{array} \right.\]
Suy ra phương trình miêu tả hình dáng nhà vòm là \[\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{25}} = 1\].
Điểm cách chân tường 5m tương ứng cách tâm 5m (vì từ tâm vòm đến tường là 10m).
Thay \[x = 5\] vào phương trình \[\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{25}} = 1\], ta tìm được \[y = \frac{{5\sqrt 3 }}{2}\].
Khi đó: \(\left\{ \begin{array}{l}a = 5\\b = 3\\c = 2\end{array} \right. \Rightarrow T = a + 2b - c = 5 + 2.3 - 2 = 9\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
a) Sai: Ta có số cách chọn ngẫu nhiên 4 quân bài là: \(C_{52}^4 = 270725\).
Suy ra số phần tử của không gian mẫu là: \(n\left( \Omega \right) = 270725\).
Vì bộ bài chỉ có 1 tứ quý Át nên số phần tử của biến cố \[A\] là: \(n\left( A \right) = 1\).
Vậy xác suất của biến cố \(A\) là \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{1}{{270725}}\].
b) Đúng: Ta có số cách chọn ngẫu nhiên 4 quân bài là: \(C_{52}^4 = 270725\).
Suy ra số phần tử của không gian mẫu là: \(n\left( \Omega \right) = 270725\).
Có \(C_4^2\) cách rút được hai quân Át, Có \(C_4^2\) cách rút được hai quân \(K\) nên số phần tử của biến cố \[B\] là: \(n\left( B \right) = C_4^2.C_4^2 = 36\).
Vậy xác suất của biến cố \(B\) là \[P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{{36}}{{270725}}\].
c) Sai: Ta có số cách chọn ngẫu nhiên 4 quân bài là: \(C_{52}^4 = 270725\).
Suy ra số phần tử của không gian mẫu là: \(n\left( \Omega \right) = 270725\).
Biến cố \(\overline C \): “ Rút không được quân Át nào”.
Có \(C_{48}^4\) cách rút bốn quân không cố quân Át nào nên số phần tử của biến cố \[\overline C \] là: \(n\left( {\overline C } \right) = C_{48}^4 = 194580\).
Vậy xác suất của biến cố \(C\) là \[P\left( C \right) = 1 - P\left( {\overline C } \right) = 1 - \frac{{n\left( {\overline C } \right)}}{{n\left( \Omega \right)}} = 1 - \frac{{194580}}{{270725}} = 1 - \frac{{38916}}{{54145}} = \frac{{15229}}{{54145}}\].
d) Đúng: Ta có số cách chọn ngẫu nhiên 4 quân bài là: \(C_{52}^4 = 270725\).
Suy ra số phần tử của không gian mẫu là: \(n\left( \Omega \right) = 270725\).
Có \(C_{13}^1\) cách chọn ra 1 tứ quý. Ứng với tứ quý này có \(C_4^2\) cách chọn ra 2 quân bài.
Có \(C_{12}^2\) cách chọn ra 2 tứ quý từ 12 tứ quý còn lại. Mỗi tứ quý này có \(C_4^1\) cách chọn ra 1 quân bài nên số phần tử của biến cố \[D\] là: \(n\left( D \right) = C_{13}^1.C_4^2.C_{12}^2.{\left( {C_4^1} \right)^2} = 82368\).
Vậy xác suất của biến cố \(D\) là \[P\left( D \right) = P\left( D \right) = \frac{{n\left( D \right)}}{{n\left( \Omega \right)}} = \frac{{82368}}{{270725}}\].
Câu 2
Lời giải
a) Đúng: Số trung bình là \(\overline x = \frac{{575 + 454 + 400 + 325 + 351 + 333 + 412}}{7} \approx 407,142857\)
b) Sai: Sắp xếp số liệu theo thứ tự không giảm \(325\,\,\,333\,\,\,351\,\,\,400\,\,\,412\;\;454\;\;575\). Trung vị của mẫu số liệu là \({M_e} = 400\)
c) Sai: Ngày 1 không là mốt nên mệnh đề sai.
d) Sai: Nếu ngày 6 có 400 lượt khách thì mốt là 400 mà không phải là ngày 3
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.