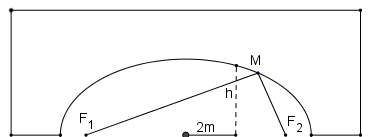
Mái vòm của một đường hầm có hình bán elip. Biết elip có tiêu cự \(8m\) và tổng các khoảng cách từ mỗi điểm trên elip đến hai tiêu cự bằng \(10m\). Gọi \(h\) là chiều cao của mái vòm tại điểm cách tâm của đường hầm \(2m\). Khi đó \(h = \frac{{a\sqrt b }}{c}\) với \(a,b,c\) là các số nguyên dương thì giá trị của biểu thức \(T = a + b + 2c\) bằng bao nhiêu?

Nếu cửa hàng bán một cuốn sách giá \(80\) nghìn đồng thì mỗi tháng khách hàng sẽ mua \(150 - 80 = 70\) cuốn sách.

Gọi \(T\left( x \right)\) là số tiền lãi của cửa hàng mỗi tháng

Ta có \(T\left( x \right) = \left( {150 - x} \right)\left( {x - 50} \right) =  - {x^2} + 200x - 7500\).

Đồ thị \(T\left( x \right)\) là một parabol có đỉnh \(I\left( {100;2500} \right)\)

Do đó lợi nhuận cao nhất khi bán 1 cuốn sách với giá \(100\)(nghìn đồng).

Khi \(T\left( x \right) = 2,1\) triệu thì ta có \( - {x^2} + 200x - 7500 = 2100 \Leftrightarrow \left[ \begin{array}{l}x = 120\\x = 80\end{array} \right.\).

Cửa hàng sẽ đạt lợi nhuận \(2,1\) triệu đồng mỗi tháng nếu mỗi tháng khách hàng mua \(150 - 80 = 70\) cuốn sách hoặc \(150 - 120 = 30\) cuốn sách.

a) Sai: Theo ước tính, nếu cửa hàng bán một cuốn sách giá \(80\) nghìn đồng thì mỗi tháng khách hàng sẽ mua \(70\) cuốn sách.

b) Đúng: Số tiền lãi của cửa hàng mỗi tháng được tính bằng công thức \(T\left( x \right) =  - {x^2} + 200x - 7500\)

c) Sai: Cửa hàng sẽ đạt lợi nhuận \(2,1\) triệu đồng mỗi tháng nếu mỗi tháng khách hàng mua \(70\) cuốn sách hoặc \(30\) cuốn sách.

d) Đúng: Nếu cửa hàng bán một cuốn sách với giá \(100\) nghìn đồng thì sẽ có lợi nhuận cao nhất.

a) Đúng: Số các xếp \(6\)bạn thành một hàng dọc là \(6!\).

b) Sai: Chọn Bình hoặc An đứng đầu hàng có 2 cách

Xếp 4 bạn còn lại có \(4!\) cách

Vậy số cách xếp 6 bạn sao cho Bình hoặc An đứng đầu hàng là \(2.4!\).

c) Đúng: Xếp Bình và An đứng cạnh nhau có 2 cách

Xếp Bình, An và 4 bạn còn lại có \(5!\) cách

Vậy có \(2.5!\) cách xếp sao cho Bình và An đứng cạnh nhau.

d) Đúng: Xếp 4 bạn còn lại có \(4!\) cách

Xếp Bình và An vào 2 trong 5 khe trống có \(A_5^2\) cách

Vậy có \(4!A_5^2\) cách xếp Bình và An không đứng cạnh nhau.