1) Tính \(A = \sqrt 9 + \sqrt {12} + \sqrt {27} - 5\sqrt 3 .\)
2) Cho biểu thức \(B = \left( {\frac{1}{{\sqrt x + 2}} + \frac{1}{{\sqrt x - 2}}} \right) \cdot \left( {\frac{{\sqrt x }}{{\sqrt x - 2}} - \frac{4}{{x - 2\sqrt x }}} \right)\) với \(x > 0\) và \(x \ne 4.\)
Rút gọn biểu thức \(B\) và tìm \(x\) để \(B < 0.\)
1) Tính \(A = \sqrt 9 + \sqrt {12} + \sqrt {27} - 5\sqrt 3 .\)
2) Cho biểu thức \(B = \left( {\frac{1}{{\sqrt x + 2}} + \frac{1}{{\sqrt x - 2}}} \right) \cdot \left( {\frac{{\sqrt x }}{{\sqrt x - 2}} - \frac{4}{{x - 2\sqrt x }}} \right)\) với \(x > 0\) và \(x \ne 4.\)
Rút gọn biểu thức \(B\) và tìm \(x\) để \(B < 0.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
1) Ta có:
\(A = \sqrt 9 + \sqrt {12} + \sqrt {27} - 5\sqrt 3 \)\( = \sqrt {{3^2}} + \sqrt {{2^2} \cdot 3} + \sqrt {{3^2} \cdot 3} - 5\sqrt 3 \)
\( = 3 + 2\sqrt 3 + 3\sqrt 3 - 5\sqrt 3 \)\( = 3 + \left( {2 + 3 - 5} \right) \cdot \sqrt 3 \)\( = 3.\)
Vậy \(A = 3.\)
2) Với \(x > 0\) và \(x \ne 4,\) ta có:
\(B = \left( {\frac{1}{{\sqrt x + 2}} + \frac{1}{{\sqrt x - 2}}} \right) \cdot \left( {\frac{{\sqrt x }}{{\sqrt x - 2}} - \frac{4}{{x - 2\sqrt x }}} \right)\)
\( = \frac{{\sqrt x - 2 + \sqrt x + 2}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} \cdot \left[ {\frac{{\sqrt x }}{{\sqrt x - 2}} - \frac{4}{{\sqrt x \left( {\sqrt x - 2} \right)}}} \right]\)
\( = \frac{{2\sqrt x }}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} \cdot \frac{{x - 4}}{{\sqrt x \left( {\sqrt x - 2} \right)}}\)
\( = \frac{{2\sqrt x \left( {x - 4} \right)}}{{\left( {x - 4} \right) \cdot \sqrt x \cdot \left( {\sqrt x - 2} \right)}} = \frac{2}{{\sqrt x - 2}}.\)
Như vậy, với \(x > 0\) và \(x \ne 4,\) thì \(B = \frac{2}{{\sqrt x - 2}}.\)
Khi đó, để \(B < 0\) thì \(\frac{2}{{\sqrt x - 2}} < 0,\) tức là \(\sqrt x - 2 < 0,\) suy ra \(\sqrt x < 2,\) nên \(x < 4.\)
Đối chiếu điều kiện \(x > 0\) và \(x \ne 4,\) ta được \(0 < x < 4.\)
Vậy với \(0 < x < 4\) thì \(B < 0.\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1) ⦁ Vẽ đồ thị hàm số \(y = - 2{x^2}.\)
|
Ta có bảng giá trị của \(y\) tương ứng với giá trị của \(x\) như sau:
Vẽ các điểm \(\left( { - 2; - 8} \right),\) \(\left( { - 1; - 2} \right),\) \(\left( {0;0} \right),\) \(\left( {1; - 2} \right),\) \(\left( {2; - 8} \right)\) thuộc đồ thị của hàm số \(y = - 2{x^2}\) trong mặt phẳng tọa độ \(Oxy.\) Vẽ đường parabol đi qua năm điểm trên, ta nhận được đồ thị hàm số \(y = - 2{x^2}\) (hình vẽ). ⦁ Vẽ đồ thị hàm số \(y = - 2x - 4.\) Cho \(x = 0\) ta có \(y = - 4.\) Đồ thị hàm số đi qua điểm \(A\left( {0; - 4} \right).\) |
Đồ thị của hàm số \(y = - 2{x^2}\) và \(y = - 2x - 4\) trên cùng một mặt phẳng tọa độ:  |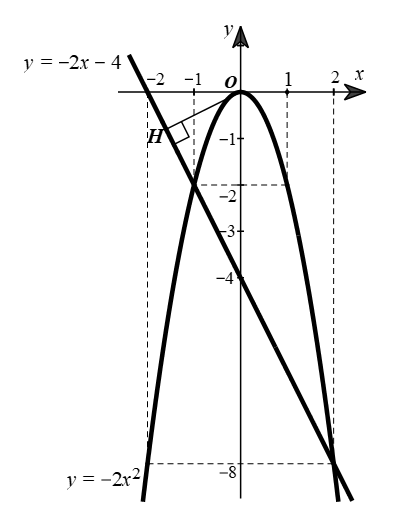
Cho \(y = 0\) ta có \(x = - 2.\) Đồ thị hàm số đi qua điểm \(B\left( { - 2;0} \right).\)
Vẽ đường thẳng đi qua hai điểm \(A\left( {0; - 4} \right)\) và \(B\left( { - 2;0} \right)\) ta được đồ thị hàm số \(y = - 2x - 4\) (hình vẽ).
2) ⦁ Gọi \(\left( {{x_0};{y_0}} \right)\) là tọa độ giao điểm (nếu có) của hai đồ thị hàm số \(y = - 2x - 4\) và \(y = - 2{x^2},\) khi đó ta có: \({y_0} = - 2{x_0} - 4\) và \({y_0} = - 2x_0^2.\)
Suy ra \( - 2{x_0} - 4 = - 2x_0^2\) hay \(x_0^2 - {x_0} - 2 = 0.\)
Số giao điểm của hai đồ thị là số nghiệm của phương trình \(x_0^2 - {x_0} - 2 = 0.\,\,\,\left( 1 \right)\)
Ta có: \(a - b + c = 1 - \left( { - 1} \right) + \left( { - 2} \right) = 0\) nên phương trình \(\left( 1 \right)\) có hai nghiệm là \({x_0} = - 1\) và \({x_0} = 2.\)
Với \({x_0} = - 1,\) ta có \({y_0} = - 2 \cdot \left( { - 1} \right) - 4 = - 2;\)
Với \({x_0} = 2,\) ta có \({y_0} = - 2 \cdot 2 - 4 = - 8.\)
Vậy tọa độ giao điểm \(C,\,\,D\) của hai đồ thị là: \(C\left( { - 1; - 2} \right)\) và \(D\left( {2; - 8} \right),\) hoặc \(C\left( {2; - 8} \right)\) và \(D\left( { - 1; - 2} \right).\)
⦁ Khoảng cách từ gốc tọa độ \(O\) đến đường thẳng \(CD\) chính là khoảng cách từ gốc tọa độ \(O\) đến đường thẳng \(y = - 2x - 4.\)
Gọi \(H\) là chân đường cao kẻ từ \(O\) xuống đường thẳng \[CD,\] ta có \(OH \bot CD.\)
Ta có \(A\left( {0; - 4} \right),\,\,B\left( { - 2;0} \right)\) suy ra \(OA = 4,\,\,OB = 2.\)
Xét \(\Delta OAB\) vuông tại \(O,\) có:
⦁ \(A{B^2} = O{A^2} + O{B^2}\) (định lí Pythagore)
Suy ra \(AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{4^2} + {2^2}} = \sqrt {20} = 2\sqrt 5 .\)
⦁ \(\sin \widehat {OBA} = \frac{{OA}}{{AB}}.\)
Xét \(\Delta OBH\) vuông tại \(H,\) có: \(\sin \widehat {OBH} = \frac{{OH}}{{OB}}.\)
Suy ra \(\frac{{OA}}{{AB}} = \frac{{OH}}{{OB}},\) do đó \(OH = \frac{{OA \cdot OB}}{{AB}} = \frac{{4 \cdot 2}}{{2\sqrt 5 }} = \frac{{4\sqrt 5 }}{5}.\)
Vậy khoảng cách từ gốc tọa độ \(O\) đến đường thẳng \(CD\) bằng \(\frac{{4\sqrt 5 }}{5}.\)
Lời giải
1) ⦁ Chứng minh tứ giác \(OCMA\) nội tiếp
Do \[MA,{\rm{ }}MC\] là tiếp tuyến của đường tròn \(\left( O \right)\) nên \(\widehat {MAO} = \widehat {MCO} = 90^\circ .\)
Do đó hai điểm \(A,\,\,C\) cùng nằm trên đường tròn đường kính \(MO.\)
Vậy tứ giác \[OCMA\] nội tiếp đường tròn đường kính \(MO.\)
⦁ Chứng minh \(HA = HC\)
Ta có \(MA = MC\) (tính chất hai tiếp tuyến cắt nhau) và \(OA = OC\) nên \(MO\) là đường trung trực của \[AC.\] Do đó \(MO \bot AC\) tại trung điểm \(H\) của \(AC.\)
Suy ra \(HA = HC.\)
2) ⦁ Chứng minh \(HE \cdot CM = HM \cdot CH\)
Xét \(\Delta ACK\) có \(HE\,{\rm{//}}\,AB\) (cùng vuông góc với \(CK)\) và \(H\) là trung điểm của \(AC\) nên \(HE\) là đường trung bình của tam giác, do đó \(HE = \frac{1}{2}AK\) hay \(AK = 2HE.\)
Do \[OCMA\] là tứ giác nội tiếp nên \(\widehat {OMC} = \widehat {OAC}\) (hai góc nội tiếp cùng chắn cung \(OC)\) hay \(\widehat {HMC} = \widehat {KAC}.\)
Xét \(\Delta MHC\) và \(\Delta AKC\) có: \[\widehat {MHC} = \widehat {AKC} = 90^\circ \] và \(\widehat {HMC} = \widehat {KAC}.\)
Do đó (g.g), suy ra \(\frac{{MH}}{{AK}} = \frac{{MC}}{{AC}}\) hay \[MH \cdot AC = MC \cdot AK.\]
Suy ra \[MH \cdot 2HC = MC \cdot 2HE\] hay \[MH \cdot HC = MC \cdot HE.\]
⦁ Chứng minh tâm đường tròn ngoại tiếp tam giác \(OKH\) nằm trên đường thẳng \(OC\)
Ta có \(\widehat {CHO} = \widehat {OKC} = 90^\circ \) nên hai điểm \(H,\,\,K\) cùng nằm trên đường tròn đường kính \(OC\)
Vậy tứ giác \[HOKC\] nội tiếp đường tròn đường kính \(OC\) nên tâm đường tròn ngoại tiếp tam giác \(OKH\) nằm trên đường thẳng \(OC.\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\widehat {MCF} = \widehat {CBF}.\)
Xét \(\Delta MCF\) và \(\Delta MBC\) có: \(\widehat {CMB}\) là góc chung, \(\widehat {MCF} = \widehat {MBC}\)
Do đó (g.g), suy ra \(\frac{{MC}}{{MB}} = \frac{{MF}}{{MC}},\) hay \(M{C^2} = MF \cdot MB.\)
Xét \(\Delta MCH\) vuông tại \(H,\) ta có \(\cos \widehat {CMH} = \frac{{MH}}{{MC}}.\)
Xét \(\Delta MCO\) vuông tại \(C,\) ta có \(\cos \widehat {CMO} = \frac{{MC}}{{MO}}.\)
Suy ra \(\frac{{MH}}{{MC}} = \frac{{MC}}{{MO}},\) hay \[M{C^2} = MH \cdot MO.\]
Do đó \(MH \cdot MO = MF \cdot MB\) nên \(\frac{{MH}}{{MB}} = \frac{{MF}}{{MO}}.\)
Xét \(\Delta MFH\) và \(\Delta MOB\) có: \(\widehat {OMB}\) là góc chung và \(\frac{{MH}}{{MB}} = \frac{{MF}}{{MO}}.\)
Do đó (c.g.c), suy ra \[\widehat {MHF} = \widehat {MBO}.\]
Mà \(\widehat {MHF} + \widehat {FHO} = 180^\circ \) (kề bù) nên \(\widehat {FHO} + \widehat {FBO} = 180^\circ .\)
|
Chứng minh bổ đề: Cho tứ giác \(ABCD\) có \(\widehat {ADC} + \widehat {ABC} = 180^\circ .\) Chứng minh tứ giác \(ABCD\) nội tiếp.
Xét \(\Delta AFD\) và \(\Delta CFK\) có: \(\widehat {AFD} = \widehat {CFK}\) (đối đỉnh) và \(\widehat {ADF} = \widehat {CKF}\) (chứng minh trên) Do đó suy ra \(\frac{{AF}}{{CF}} = \frac{{DF}}{{KF}}\) nên \(\frac{{AF}}{{DF}} = \frac{{CF}}{{KF}}.\) Xét \(\Delta DFK\) và \(\Delta AFC\) có: \(\frac{{AF}}{{DF}} = \frac{{CF}}{{KF}}\) và \[\widehat {DFK} = \widehat {AFC}\] (đối đỉnh) Do đó suy ra \(\widehat {FDK} = \widehat {FAC}.\,\,\,\left( 4 \right)\) ⦁ Ta có \(\widehat {ACK}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ACK} = 90^\circ ,\) do đó \(\Delta ACK\) vuông tại \(C,\) suy ra \(\widehat {FAC} + \widehat {AKC} = 90^\circ .\,\,\,\left( 5 \right)\) Từ \(\left( 3 \right),\,\,\left( 4 \right),\,\,\left( 5 \right)\) suy ra \(\widehat {ADC} + \widehat {FDK} = 90^\circ \) hay \(\widehat {ADK} = 90^\circ .\) Khi đó \(\Delta ADK\) vuông tại \(D\) nên điểm \(D\) nằm trên đường tròn đường kính \(AK.\) Suy ra tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) đường kính \(AK.\) |
Áp dụng bổ đề trên cho tứ giác \(OHFB\) có \(\widehat {FHO} + \widehat {FBO} = 180^\circ ,\) suy ra tứ giác \(OHFB\) nội tiếp đường tròn, do đó \(\widehat {HFB} + \widehat {HOB} = 180^\circ .\)
Mà \(\widehat {HOB} + \widehat {HOA} = 180^\circ \) nên \(\widehat {HFB} = \widehat {HOA}.\)
Lại có \(\widehat {HOA} = \widehat {ACK}\) (cùng phụ với \(\widehat {KAC})\) nên \(\widehat {HFB} = \widehat {ACK}\) hay \(\widehat {HFE'} = \widehat {HCE'}.\)
|
Chứng minh bổ đề: Cho tứ giác \(ABCD\) có \(\widehat {ACB} = \widehat {ADB}.\) Chứng minh tứ giác \(ABCD\) là tứ giác nội tiếp.
Xét \(\Delta AFD\) và \(\Delta BFK\) có: \(\widehat {AFD} = \widehat {BFK}\) (đối đỉnh) và \(\widehat {ADF} = \widehat {BKF}\) (chứng minh trên) Do đó suy ra \(\frac{{AF}}{{BF}} = \frac{{DF}}{{KF}}\) nên \(\frac{{AF}}{{DF}} = \frac{{BF}}{{KF}}.\) Xét \(\Delta DFK\) và \(\Delta AFB\) có: \(\frac{{AF}}{{DF}} = \frac{{BF}}{{KF}}\) và \[\widehat {DFK} = \widehat {AFB}\] (đối đỉnh) Do đó suy ra \(\widehat {FDK} = \widehat {FAB}.\,\,\,\left( 7 \right)\) ⦁ Ta có \(\widehat {ABK}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ABK} = 90^\circ ,\) do đó \(\Delta ABK\) vuông tại \(B,\) suy ra \(\widehat {FAB} + \widehat {AKB} = 90^\circ .\,\,\,\left( 8 \right)\) Từ \(\left( 6 \right),\,\,\left( 7 \right),\,\,\left( 8 \right)\) suy ra \(\widehat {ADB} + \widehat {FDK} = 90^\circ \) hay \(\widehat {ADK} = 90^\circ .\) Khi đó \(\Delta ADK\) vuông tại \(D\) nên điểm \(D\) nằm trên đường tròn đường kính \(AK.\) Suy ra tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) đường kính \(AK.\) |
Áp dụng bổ đề trên cho tứ giác \(HFCE'\) có \(\widehat {HFE'} = \widehat {HCE'},\) suy ra tứ giác \(HFCE'\) nội tiếp đường tròn, do đó \[\widehat {E'HC} = \widehat {E'FC}\] (hai góc nội tiếp cùng chắn cung \(E'C)\)
Mà \[\widehat {E'FC} = \widehat {BFC} = \widehat {BAC}\] (hai góc nội tiếp cùng chắn cung \(BC\) của đường tròn \(\left( O \right))\) nên \(\widehat {E'HC} = \widehat {BAC},\) lại có hai góc này ở vị trí đồng vị nên \(HE'{\rm{ // }}AB.\)
Xét \(\Delta ACK\) có \(HE'{\rm{ // }}AB\) và \(H\) là trung điểm \(AC\) nên \[HE'\] là đường trung bình của tam giác, do đó \(E'\) là trung điểm \(CK\)
Như vậy, điểm \(E\) và điểm \[E'\] trùng nhau.
Vậy ba điểm \(M,\,\,E,\,\,B\) thẳng hàng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập