Cho parabol \(\left( P \right):y = - {x^2}\) và đường thẳng \(\left( d \right):y = - 3x + 2\).
1) Vẽ \(\left( P \right)\) và \(\left( d \right)\) trên cùng hệ trục tọa độ.
2) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.
Cho parabol \(\left( P \right):y = - {x^2}\) và đường thẳng \(\left( d \right):y = - 3x + 2\).
1) Vẽ \(\left( P \right)\) và \(\left( d \right)\) trên cùng hệ trục tọa độ.
2) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Vẽ \(\left( P \right)\) và \(\left( d \right)\) trên cùng hệ trục tọa độ.
|
* Vẽ \(\left( P \right)\): Ta có bảng giá trị sau:
Do đó, đồ thị hàm số là đường cong đi qua các điểm \(O\left( {0\,;\,\,0} \right);\,\,A\left( { - 2\,;\,\, - 4} \right);\,\,\)\(B\left( { - 1\,;\,\, - 1} \right);\) \(C\left( {1\,;\,\, - 1} \right);\) \(\,D\left( {2\,;\,\, - 4} \right).\) * Vẽ \(\left( d \right)\): Ta có bảng giá trị:
Do đó, đồ thị hàm số là đường thẳng đi qua các điểm \(E\left( {0\,;\,\,2} \right);\,\,C\left( {1\,;\,\, - 1} \right).\) |
Ta vẽ được đồ thị hàm số \(y = - {x^2}\) và \(y = - 3x + 2\) như sau:  |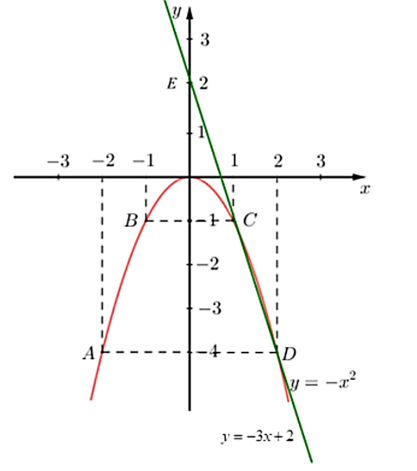
b) Phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là
\( - {x^2} = 3x + 2\)
\( - {x^2} + 3x - 2 = 0\)
\(x = 1\) hoặc \(x = 2\)
Với \(x = 1\) thì \(y = - 1\);
Với \(x = 2\) thì \(y = - 4\).
Vậy tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là \(\left( {1\,;\,\, - 1} \right)\) và \(\left( {2\,;\, - 4} \right)\).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
a) Vì \(AB,\,\,AC\) là tiếp tuyến nên \(\widehat {ABO} = \widehat {ACO} = 90^\circ \). Xét tứ giác \(ABOC\) có \(\widehat {ABO} + \widehat {ACO} = 90^\circ + 90^\circ = 180^\circ .\) Mà hai góc này ở vị trí đối diện nên tứ giác \(ABOC\) nội tiếp. |
 |
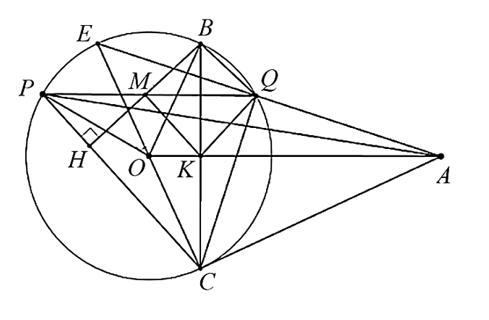Ta có \(AB = AC\) (tính chất hai tiếp tuyến cắt nhau); \(OB = OC = R\).
Suy ra \(AO\) là đường trung trực của \(BC\) (đpcm).
b) Do \(K\) là trung điểm \(BC,M\) là trung điểm \(BH\) nên \(KM\) là đường trung bình \(\Delta BCH.\)
Suy ra \(KM\,{\rm{//}}\,CH\) nên \(\widehat {QMK} = \widehat {QPC}\) (đồng vị)
Vì \(\Delta OCQ\) cân tại \(O\) nên \(\widehat {OCQ} = \widehat {OQC}.\)
Suy ra \(\widehat {OCQ} = \widehat {OQC} = \frac{{180^\circ - \widehat {COQ}}}{2} = 90^\circ - \frac{{\widehat {COQ}}}{2}.\)
Vì \[AC\] là tiếp tuyến với đường tròn \[\left( O \right)\] tại điểm \[C\] nên \(OC \bot CA\) hay \(\widehat {OCA} = 90^\circ \).
Suy ra \[\widehat {ACQ} = 90^\circ - \widehat {OCQ}\]\[ = 90^\circ - \left( {90^\circ - \frac{{\widehat {COQ}}}{2}} \right) = \frac{{\widehat {COQ}}}{2}.\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\]
Mặt khác nên \[\widehat {QPC} = \frac{{\widehat {COQ}}}{2}.\,\,\,\,\left( 2 \right)\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \(\widehat {QCA} = \widehat {QPC}\). Vậy \(\widehat {QMK} = \widehat {QCA}\).
c) Kẻ \(AQ\) cắt \(\left( O \right)\) tại \(E.\)
Xét \(\Delta ACQ\) và \(\Delta AEC\) có \(\widehat {CAE}\) chung; .
Do đó
Suy ra \(\frac{{AC}}{{AE}} = \frac{{AQ}}{{AC}}\) hay
Xét \(\Delta ACK\) và \(\Delta AOC\) có \(\widehat {AKC} = \widehat {ACO} = 90^\circ \); \(\widehat {ACK} = \widehat {AOC}\) (cùng phụ \(\widehat {OCK}\,)\).
Do đó .
Suy ra \(\frac{{AC}}{{AK}} = \frac{{AO}}{{AC}}\) hay
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(AK \cdot AO = AE \cdot AQ\) hay \(\frac{{AK}}{{AQ}} = \frac{{AE}}{{AO}}\).
Xét \(\Delta AKQ\) và \(\Delta AEO\) có \(\widehat {OAE}\) chung; \(\frac{{AK}}{{AQ}} = \frac{{AE}}{{AO}}\) (chứng minh trên).
Do đó . Suy ra \(\widehat {AKQ} = \widehat {AEO}\).
|
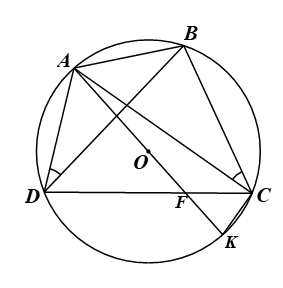
Chứng minh bổ đề: Cho tứ giác \(ABCD\) có \(\widehat {ACB} = \widehat {ADB}.\) Chứng minh tứ giác \(ABCD\) là tứ giác nội tiếp.
Xét \(\Delta AFD\) và \(\Delta BFK\) có: \(\widehat {AFD} = \widehat {BFK}\) (đối đỉnh) và \(\widehat {ADF} = \widehat {BKF}\) (chứng minh trên) Do đó suy ra \(\frac{{AF}}{{BF}} = \frac{{DF}}{{KF}}\) nên \(\frac{{AF}}{{DF}} = \frac{{BF}}{{KF}}.\) Xét \(\Delta DFK\) và \(\Delta AFB\) có: \(\frac{{AF}}{{DF}} = \frac{{BF}}{{KF}}\) và \[\widehat {DFK} = \widehat {AFB}\] (đối đỉnh) Do đó suy ra \(\widehat {FDK} = \widehat {FAB}.\,\,\,\left( 7 \right)\) ⦁ Ta có \(\widehat {ABK}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ABK} = 90^\circ ,\) do đó \(\Delta ABK\) vuông tại \(B,\) suy ra \(\widehat {FAB} + \widehat {AKB} = 90^\circ .\,\,\,\left( 8 \right)\) Từ \(\left( 6 \right),\,\,\left( 7 \right),\,\,\left( 8 \right)\) suy ra \(\widehat {ADB} + \widehat {FDK} = 90^\circ \) hay \(\widehat {ADK} = 90^\circ .\) Khi đó \(\Delta ADK\) vuông tại \(D\) nên điểm \(D\) nằm trên đường tròn đường kính \(AK.\) Suy ra tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) đường kính \(AK.\) |
Áp dụng bổ đề trên cho tứ giác \(ACKQ\) có \(\widehat {AKQ} = \widehat {AEO}\) nên tứ giác \(ACKQ\) nội tiếp.
Suy ra \(\widehat {AQC} = \widehat {AKC} = 90^\circ \).
Do \(\widehat {AQC} = 90^\circ \) nên \(\widehat {CQE} = 90^\circ \) nên \(CE\) là đường tròn đường kính của \[\left( O \right)\].
Suy ra ba điểm \(E,\,\,O,\,\,C\) thẳng hàng nên \(\widehat {CPQ} = \widehat {CEQ}\).
Ta có \(\tan \widehat {CPQ} = \tan \widehat {CEQ} = \frac{{AC}}{{EC}} = \frac{{AC}}{{2R}}\).
Do đó \(AC = 2R\tan \widehat {ACQ} = 2R\tan \widehat {CPQ}\) (đpcm).
![Một khu vườn hình chữ nhật có chiều dài là \[30{\rm{ m}}\] và chiều rộng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid4-1766231096.png)
Lời giải
|
a) Gọi các phần còn lại lần lượt là \(A\) và \(B\) (như hình vẽ). Biểu thức biểu thị cạnh còn thiếu của \(A\) là: \(20 - y.\) Biểu thức biểu thị diện tích phần \(A\) là: \({S_A} = 15\left( {20 - y} \right) = 300 - 15y.\) |
![Một khu vườn hình chữ nhật có chiều dài là \[30{\rm{ m}}\] và chiều rộng (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid3-1766231067.png) |
Biểu thức biểu thị cạnh còn thiếu của \(B\) là: \(30 - 15 - x = 15 - x.\)
Biểu thức biểu thị diện tích phần \(B\) là: \({S_B} = 20\left( {15 - x} \right) = 300 - 20x.\)
Vậy biểu thức là \(15\left( {20 - y} \right) + 20\left( {15 - x} \right) = 600 - 20x - 15y\).
b) Thay \(x = 2,4\) và \(y = 1,8\) vào \(S,\) ta được:
.
Vậy diện tích phần còn lại của khu vườn là \(525\,\,{{\rm{m}}^{\rm{2}}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập