Tìm tập nghiệm của bất phương trình \( - 2{x^2} - 3x + 2 > 0\) là
A. \(\left( { - 2\,;\,\frac{1}{2}} \right)\).
B. \(\left( { - \infty & \,;\, - \frac{1}{2}} \right) \cup \left( {2\,;\, + \infty } \right)\).
Quảng cáo
Trả lời:
Đáp án đúng là A
Đặt \(f\left( x \right) = - 2{x^2} - 3x + 2\). \(f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = \frac{1}{2}\end{array} \right.\).
Bảng xét dấu của \(f\left( x \right) = - 2{x^2} - 3x + 2\) là
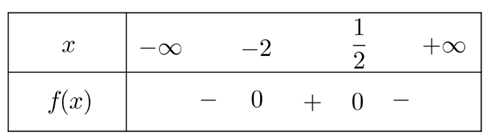
Từ bảng xét dấu suy ra tập nghiệm của bất phương trình là \(\left( { - 2\,;\,\frac{1}{2}} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng: \(\left( P \right)\) đi qua hai điểm \(M\left( {1;0} \right)\) và \(N\left( { - 1;0} \right)\) nên ta được
\(\left\{ \begin{array}{l}a + b + 2 = 0\\a - b + 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 2\\b = 0\end{array} \right. \Rightarrow a + 2024b = - 2\).
b) Sai: \(\left( P \right)\) có trục đối xứng là \(x = 1 \Rightarrow - \frac{b}{{2a}} = 1 \Rightarrow 2a + b = 0\;\left( 1 \right)\)
Mặt khác \(\left( P \right)\) đi qua điểm \(E\left( { - 1;5} \right)\) nên \(a - b + 2 = 5 \Leftrightarrow a - b = 3\;\left( 2 \right)\)
Từ \(\left( 1 \right),\;\left( 2 \right)\) suy ra \(a = 1,\;b = - 2\). Do đó \(2a + b = 0\).
c) Sai: \(\left( P \right)\) đi qua điểm \(F\left( { - 1;6} \right)\) nên \(a - b + 2 = 6 \Leftrightarrow a - b = 4 \Leftrightarrow a = b + 4\;\left( 3 \right)\)
Lại có \(\left( P \right)\) có tung độ đỉnh bằng \( - \frac{1}{4}\) nên
\( - \frac{\Delta }{{4a}} = - \frac{1}{4} \Rightarrow \frac{{{b^2} - 4ac}}{{4a}} = \frac{1}{4} \Rightarrow {b^2} - 8a = a \Rightarrow {b^2} - 9a = 0\;\left( 4 \right)\)
Thay \(\left( 3 \right)\) vào \(\left( 4 \right)\) được \({b^2} - 9\left( {b + 4} \right) = 0 \Leftrightarrow {b^2} - 9b - 36 = 0 \Leftrightarrow \left[ \begin{array}{l}b = - 3 \Rightarrow a = 1\\b = 12 \Rightarrow a = 16\end{array} \right.\)
Suy ra \(ab = - 3\) hoặc \(ab = 192\).
d) Đúng: Vì \(\left( P \right)\) có đỉnh là điểm \(S\left( { - 1; - \frac{3}{2}} \right)\) nên hoành độ đỉnh \(x = - 1 = - \frac{b}{{2a}} \Rightarrow 2a - b = 0\;\left( 5 \right)\)
Lại có \(\left( P \right)\) đi qua \(S\left( { - 1; - \frac{3}{2}} \right)\) nên \(a - b + 2 = - \frac{3}{2} \Leftrightarrow a - b = - \frac{7}{2}\;\left( 6 \right)\)
Từ \(\left( 5 \right),\;\left( 6 \right)\) ta được \(a = \frac{7}{2},\;b = 7 \Rightarrow 2a + b = 14\).
Lời giải
a) Sai: Xếp tùy ý 9 bạn lên hàng ghé nằm ngang, ta có \(9! = 362880\) (cách).
b) Đúng: Xếp bạn An ngồi chính giữa, hoán vị 8 bạn còn lại ta có \(8! = 40320\) (cách).
c) Đúng: Xếp chỗ cho An và Bình ngồi cạnh nhau (thành nhóm \(X\)), số cách xếp trong \(X\) là \(2!\)
Số cách xếp nhóm \(X\) với 7 người còn lại (ta xem là hoán vị của 8 phần từ), số cách xếp là 8!.
Số cách xếp hàng thỏa mãn là \(2!8! = 80640\) (cách).
d) Đúng: Số cách xếp 9 bạn vào 9 chỗ là 9 ! cách. Vậy số cách xếp để An và Binh không ngồi cạnh nhau là: \(9! - 2!8! = 282240\) (cách).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[S = \left\{ 3 \right\}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.