(2,5 điểm) .
Ngày \[1/1/2016\], ông Tư mang \[50\,000\,000\] đồng vào ngân hàng gửi tiết kiệm với lãi suất \[7\% \] năm. Đến ngày[1/1/2017\]ông Tư đến ngân hàng không rút lãi ra mà gửi thêm vào \[26\,500\,000\] đồng với kì hạn 1 năm nhưng lãi suất hiện tại của ngân hàng là \[7,5\% \] năm. Ngày \[1/1/2018\]vì bận công việc nên ông không đến rút tiền lãi được và tiền lãi sẽ được cộng vào tiền gốc để tính lãi kép. Hỏi nếu vào ngày \[1/1/2019\]ông Tư đến rút cả gốc lẫn lãi thì được tất cả bao nhiêu tiền?
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 8 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
w Số tiền lãi sau \[1\] năm gửi ngân hàng là:
\[50\,000\,000\,\, \cdot \,\,\frac{7}{{100}}\, = \,3\,500\,000\] (đồng)
w Từ ngày \[1/1/2017\]ông Tư cho ngân hàng vay số tiền là:
\[50\,000\,000\,\, + \,3\,500\,000\,\, + \,\,26\,500\,000\,\, = \,\,80\,000\,000\] (đồng)
w Theo công thức lãi kép
Số tiền ông Tư sẽ rút cả vốn lẫn lãi vào ngày \[1/1/2019\]là:
\[80\,000\,000\,\, \cdot \,{\left( {1\, + \,\frac{{7,5}}{{100}}} \right)^2}\, = \,\,92\,450\,000\] (đồng)
Câu hỏi cùng đoạn
Câu 2:
Một đội xe cần chở \[480\] tấn hàng, khi sắp khởi hành đội được điều thêm \[3\] xe nữa nên mỗi xe chở ít hơn dự định \[8\] tấn. Hỏi lúc đầu đội có bao nhiêu chiếc xe? Biết rằng các xe chở số hàng như nhau.
Giải bởi Vietjack
Gọi số xe của đội ban đầu là \[x\] (xe, \(x \in {N^*}\))
Số xe thực tế là:\[x + 3\] ( xe)
Dự định mỗi xe phải chở số hàng là: (tấn)
Thực tế mỗi xe phải chở số hàng là : \(\frac{{480}}{{x + 3}}\) (tấn)
Vì mỗi xe chở ít hơn dự định 8 tấn nên ta có phương trình:
\(\frac{{480}}{x} - \frac{{480}}{{x + 3}} = 8\)
Giải phương trình tìm được \[x = 12\](TM)
Vậy ban đầu đội có 12 xe.
Câu 3:
Biết phương trình \[2{x^2} + 4x + m = 0\]\(( * )\) (\[m\]là tham số) có \[1\] nghiệm bằng \[1\]. Tính tổng bình phương hai nghiệm của phương trình.
Giải bởi Vietjack
Vì phương trình có một nghiệm bằng \[1\] nên ta có: \[2\,.\,1 + 4\,.\,1 + m = 0\,\,suy\,\,ra\,\,m = - 6\]
Với \[\,m = - 6\] phương trình \(( * )\) có dạng: \[2{x^2} + 4x\, - \,6 = 0\]
Ta có \[a\,\, + \,\,b\,\, + \,\,c\,\, = \,\,2\,\, + \,4\,\, - \,\,6\,\, = \,0\]
Suy ra phương trình có 2 nghiệm: \[{x_1} = \,1,\,\,{x_2}\, = \, - 6\]
Vậy tổng bình phương \[2\] nghiệm là: \[\,{1^2} + \,\,{( - 6)^2}\, = \,\,1\,\, + \,\,36\,\, = \,\,37\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Một thùng đựng nước có dạng hình trụ chiều cao là \[35\,cm\] đường kính đáy \[30\,cm\].
a) Tính thể tích của thùng.
b) Người ta sử dụng thùng trên để múc nước đổ vào một bể chứa có dung tích \(1\;{m^3}\). Hỏi cần phải đổ ít nhất bao nhiêu thùng thì đầy bể chứa ? Biết rằng mỗi lần xách người ta chỉ đổ đầy \(90{\rm{\% }}\) thùng để nước không đổ ra ngoài.
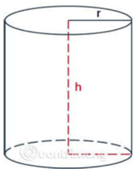
a) Tính thể tích của thùng.
b) Người ta sử dụng thùng trên để múc nước đổ vào một bể chứa có dung tích \(1\;{m^3}\). Hỏi cần phải đổ ít nhất bao nhiêu thùng thì đầy bể chứa ? Biết rằng mỗi lần xách người ta chỉ đổ đầy \(90{\rm{\% }}\) thùng để nước không đổ ra ngoài.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Bán kính đáy hình trụ là \(R = 30\,\,:2 = 15\,\left( {cm} \right)\).
Thể tích trụ: \(V = \pi {R^2}h = \pi \,.\,{15^2}.\,35 = 7875\pi \approx 24728\,\left( {c{m^3}} \right)\)
b) Thể tích nước mỗi lần xách là: \(24728\,.\,90\% = 22255\,\left( {c{m^3}} \right) = 0,022255\,\left( {{m^3}} \right)\).
Số thùng ít nhất cần đổ để đầy bể là:\(1\,\,:\,\,0,022255\,\, = \,\,44,9337..\) nên số thùng cần là \[45\] thùng
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Các nhóm \[\left[ {70;80} \right),\,\,\left[ {80;90} \right),\,\,\left[ {90;100} \right),\,\,\left[ {100;110} \right),\,\,\left[ {110;120} \right).\]) có tần số lần lượt là: \[n{}_1\, = \,3\], , \[n{}_2\, = \,6\], \[{n_3}\, = \,12\], \[{n_4}\, = \,5\], \[n{}_5\, = \,4\].
b)
|
Nhóm |
Tần số \[\left( n \right)\] |
|
\[\left[ {70\,;\,80} \right)\] |
\[3\] |
|
\[\left[ {80\,;\,90} \right)\] |
\[6\] |
|
\[\left[ {90\,;\,100} \right)\] |
\[12\] |
|
\[\left[ {100\,;\,110} \right)\] |
\[5\] |
|
\[\left[ {110\,;\,120} \right)\] |
\[4\] |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập