Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 8
74 người thi tuần này 4.6 143 lượt thi 9 câu hỏi 120 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Đoạn văn 1
Lời giải
a) Các nhóm \[\left[ {70;80} \right),\,\,\left[ {80;90} \right),\,\,\left[ {90;100} \right),\,\,\left[ {100;110} \right),\,\,\left[ {110;120} \right).\]) có tần số lần lượt là: \[n{}_1\, = \,3\], , \[n{}_2\, = \,6\], \[{n_3}\, = \,12\], \[{n_4}\, = \,5\], \[n{}_5\, = \,4\].
b)
|
Nhóm |
Tần số \[\left( n \right)\] |
|
\[\left[ {70\,;\,80} \right)\] |
\[3\] |
|
\[\left[ {80\,;\,90} \right)\] |
\[6\] |
|
\[\left[ {90\,;\,100} \right)\] |
\[12\] |
|
\[\left[ {100\,;\,110} \right)\] |
\[5\] |
|
\[\left[ {110\,;\,120} \right)\] |
\[4\] |
Lời giải
a) Các cách chọn có thể có là: đỏ \[1\] và vàng, đỏ \[2\] và vàng, đỏ \[3\] và vàng, đỏ \[1\] và đỏ \[2\], đỏ \[2\]và đỏ \[3\], đỏ \[1\] và đỏ \[3\].
b) Có \[3\] kết quả thuận lợi cho biến cố R là: đỏ \[1\] và vàng, đỏ \[2\] và vàng, đỏ \[3\] và vàng.
Vậy \(P\left( R \right) = \frac{3}{6} = \frac{1}{2}\).
Có tất cả \[4\] kết quả thuận lợi cho biến cố \[T\].
Vậy\(P\left( T \right) = \frac{4}{6} = \frac{2}{3}\) .
Lời giải
1) Tính giá trị của biểu thức \(A\) khi \(x = 9\).
Thay \(x = 9\)(tmđk) vào biểu thức \(A\) ta được
\(A = \frac{{\sqrt 9 }}{{\sqrt 9 + 2}} = \frac{3}{5}\)
2) Chứng minh \(B = \frac{3}{{\sqrt x + 2}}\). với \(x \ge 0,\,\,x \ne 4\) ta có:
\(B = \frac{5}{{\sqrt x - 2}} - \frac{{16 + 2\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\)
\(B = \frac{{5\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} - \frac{{16 + 2\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\)
\(B = \frac{{3\sqrt x - 6}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\)
\(B = \frac{3}{{\sqrt x + 2}}\)
a. Tìm giá trị nguyên lớn nhất của \(x\) để \(5A + B \le 3\).
Với \(x \ge 0,\,\,x \ne 4\) ta có: \(5A + B = \frac{{5\sqrt x + 3}}{{\sqrt x + 2}}\)
Để \(5A + B \le 3\) khi \(\frac{{5\sqrt x + 3}}{{\sqrt x + 2}} \le 3\)
\(\frac{{5\sqrt x + 3}}{{\sqrt x + 2}} - 3 \le 0\)
\(\frac{{5\sqrt x + 3}}{{\sqrt x + 2}} - \frac{{3\left( {\sqrt x + 2} \right)}}{{\sqrt x + 2}} \le 0\)
\(\begin{array}{l}\frac{{5\sqrt x + 3 - 3\sqrt x - 6}}{{\sqrt x + 2}} \le 0\\\frac{{2\sqrt x - 3}}{{\sqrt x + 2}} \le 0\\0 \le x \le \frac{9}{4}\end{array}\)
Vậy giá trị nguyên lớn nhất của x thỏa mãn yêu cầu là \(x = 2\).
Lời giải
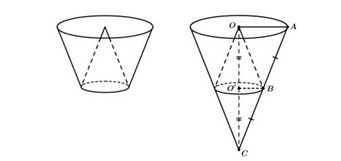
- Đường sinh \[AB\] cắt trục\[OO'\] tại \[C\]. Khi đó hai hình nón có đỉnh \[O\], \[C\] có chung đáy là hình tròn \[\left( {{O^'}} \right)\]có thể tích bằng nhau
- Gọi \[{V_1}\] là thể tích hình nón đỉnh \[C\], đáy là hình tròn \[\left( {{O^'}} \right)\] ; \[{V_2}\] là thể tích hình nón đỉnh \[O\], đáy là hình tròn \[\left( {{O^'}} \right)\]; \[V\] là thể tích hình nón đỉnh \[C\], đáy là hình tròn \[\left( O \right)\] ; \[{V_n}\, = \,12\] là thể tích nước đổ vào
- Ta có:
\[\begin{array}{l}\frac{{{V_1}}}{V} = \,\frac{{\frac{1}{3}\,\, \cdot \,CO' \cdot \,\,\pi \cdot O'{B^2}}}{{\frac{1}{3} \cdot \,\,CO \cdot \,\,\pi \cdot O{A^2}}} = \,\frac{{CO'}}{{CO}} \cdot \,{\left( {\frac{{O'B}}{{OA}}} \right)^2} = \frac{1}{2} \cdot {\left( {\frac{1}{2}} \right)^2} = \frac{1}{8}\\Suy\,\,ra\,\,{V_1} = {V_2} = \frac{1}{8}V\,\,(\,1\,)\end{array}\]
- Do đó thể tích nước đổ vào là: \[{V_n} = \frac{6}{8}V\,\,(\,2\,)\,\,\]( vì \[{V_1} + {V_2} + {V_n} = \,V\])
- Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \[{V_1} = {V_2} = \frac{1}{6}{V_n} = \frac{1}{6} \cdot 12 = \,2\,\]( lít )
- Vậy thể tích của phễu là \[2\] lít
Đoạn văn 2
Lời giải
w Số tiền lãi sau \[1\] năm gửi ngân hàng là:
\[50\,000\,000\,\, \cdot \,\,\frac{7}{{100}}\, = \,3\,500\,000\] (đồng)
w Từ ngày \[1/1/2017\]ông Tư cho ngân hàng vay số tiền là:
\[50\,000\,000\,\, + \,3\,500\,000\,\, + \,\,26\,500\,000\,\, = \,\,80\,000\,000\] (đồng)
w Theo công thức lãi kép
Số tiền ông Tư sẽ rút cả vốn lẫn lãi vào ngày \[1/1/2019\]là:
\[80\,000\,000\,\, \cdot \,{\left( {1\, + \,\frac{{7,5}}{{100}}} \right)^2}\, = \,\,92\,450\,000\] (đồng)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Câu 8
Một thùng đựng nước có dạng hình trụ chiều cao là \[35\,cm\] đường kính đáy \[30\,cm\].
a) Tính thể tích của thùng.
b) Người ta sử dụng thùng trên để múc nước đổ vào một bể chứa có dung tích \(1\;{m^3}\). Hỏi cần phải đổ ít nhất bao nhiêu thùng thì đầy bể chứa ? Biết rằng mỗi lần xách người ta chỉ đổ đầy \(90{\rm{\% }}\) thùng để nước không đổ ra ngoài.
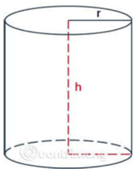
a) Tính thể tích của thùng.
b) Người ta sử dụng thùng trên để múc nước đổ vào một bể chứa có dung tích \(1\;{m^3}\). Hỏi cần phải đổ ít nhất bao nhiêu thùng thì đầy bể chứa ? Biết rằng mỗi lần xách người ta chỉ đổ đầy \(90{\rm{\% }}\) thùng để nước không đổ ra ngoài.

Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Cho tam giác \(ABC\) nhọn nội tiếp đường tròn \(\left( O \right)\). \(AD\), \(BE\), \(CF\) là ba đường cao của tam giác \(ABC\) cắt nhau tại \(H\).
a ) Chứng minh bốn điểm \(A,\,F,\,H,\,E\) cùng thuộc một đường tròn.
b ) Kẻ đường kính \(AM\) của đường tròn \(\left( O \right)\). Chứng minh \[AD.AM = AB.AC\]
c ) Gọi \(P\) là giao điểm của \(AH\) và \[{\rm{EF}}\]. \(I\) là giao điểm của \(AM\) và \(BC\). \(K\) là trung điểm của \(BC\). Chứng minh: \(H,\,K,\,M\) thẳng hàng và \(PI//HK\) .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.