(2,5 điểm) .
Ngày \[1/1/2016\], ông Tư mang \[50\,000\,000\] đồng vào ngân hàng gửi tiết kiệm với lãi suất \[7\% \] năm. Đến ngày[1/1/2017\]ông Tư đến ngân hàng không rút lãi ra mà gửi thêm vào \[26\,500\,000\] đồng với kì hạn 1 năm nhưng lãi suất hiện tại của ngân hàng là \[7,5\% \] năm. Ngày \[1/1/2018\]vì bận công việc nên ông không đến rút tiền lãi được và tiền lãi sẽ được cộng vào tiền gốc để tính lãi kép. Hỏi nếu vào ngày \[1/1/2019\]ông Tư đến rút cả gốc lẫn lãi thì được tất cả bao nhiêu tiền?
Quảng cáo
Trả lời:
w Số tiền lãi sau \[1\] năm gửi ngân hàng là:
\[50\,000\,000\,\, \cdot \,\,\frac{7}{{100}}\, = \,3\,500\,000\] (đồng)
w Từ ngày \[1/1/2017\]ông Tư cho ngân hàng vay số tiền là:
\[50\,000\,000\,\, + \,3\,500\,000\,\, + \,\,26\,500\,000\,\, = \,\,80\,000\,000\] (đồng)
w Theo công thức lãi kép
Số tiền ông Tư sẽ rút cả vốn lẫn lãi vào ngày \[1/1/2019\]là:
\[80\,000\,000\,\, \cdot \,{\left( {1\, + \,\frac{{7,5}}{{100}}} \right)^2}\, = \,\,92\,450\,000\] (đồng)
Câu hỏi cùng đoạn
Câu 2:
Một đội xe cần chở \[480\] tấn hàng, khi sắp khởi hành đội được điều thêm \[3\] xe nữa nên mỗi xe chở ít hơn dự định \[8\] tấn. Hỏi lúc đầu đội có bao nhiêu chiếc xe? Biết rằng các xe chở số hàng như nhau.
Gọi số xe của đội ban đầu là \[x\] (xe, \(x \in {N^*}\))
Số xe thực tế là:\[x + 3\] ( xe)
Dự định mỗi xe phải chở số hàng là: (tấn)
Thực tế mỗi xe phải chở số hàng là : \(\frac{{480}}{{x + 3}}\) (tấn)
Vì mỗi xe chở ít hơn dự định 8 tấn nên ta có phương trình:
\(\frac{{480}}{x} - \frac{{480}}{{x + 3}} = 8\)
Giải phương trình tìm được \[x = 12\](TM)
Vậy ban đầu đội có 12 xe.
Câu 3:
Biết phương trình \[2{x^2} + 4x + m = 0\]\(( * )\) (\[m\]là tham số) có \[1\] nghiệm bằng \[1\]. Tính tổng bình phương hai nghiệm của phương trình.
Vì phương trình có một nghiệm bằng \[1\] nên ta có: \[2\,.\,1 + 4\,.\,1 + m = 0\,\,suy\,\,ra\,\,m = - 6\]
Với \[\,m = - 6\] phương trình \(( * )\) có dạng: \[2{x^2} + 4x\, - \,6 = 0\]
Ta có \[a\,\, + \,\,b\,\, + \,\,c\,\, = \,\,2\,\, + \,4\,\, - \,\,6\,\, = \,0\]
Suy ra phương trình có 2 nghiệm: \[{x_1} = \,1,\,\,{x_2}\, = \, - 6\]
Vậy tổng bình phương \[2\] nghiệm là: \[\,{1^2} + \,\,{( - 6)^2}\, = \,\,1\,\, + \,\,36\,\, = \,\,37\]
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Một thùng đựng nước có dạng hình trụ chiều cao là \[35\,cm\] đường kính đáy \[30\,cm\].
a) Tính thể tích của thùng.
b) Người ta sử dụng thùng trên để múc nước đổ vào một bể chứa có dung tích \(1\;{m^3}\). Hỏi cần phải đổ ít nhất bao nhiêu thùng thì đầy bể chứa ? Biết rằng mỗi lần xách người ta chỉ đổ đầy \(90{\rm{\% }}\) thùng để nước không đổ ra ngoài.
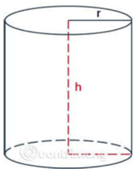
Một thùng đựng nước có dạng hình trụ chiều cao là \[35\,cm\] đường kính đáy \[30\,cm\].
a) Tính thể tích của thùng.
b) Người ta sử dụng thùng trên để múc nước đổ vào một bể chứa có dung tích \(1\;{m^3}\). Hỏi cần phải đổ ít nhất bao nhiêu thùng thì đầy bể chứa ? Biết rằng mỗi lần xách người ta chỉ đổ đầy \(90{\rm{\% }}\) thùng để nước không đổ ra ngoài.

Lời giải
a) Bán kính đáy hình trụ là \(R = 30\,\,:2 = 15\,\left( {cm} \right)\).
Thể tích trụ: \(V = \pi {R^2}h = \pi \,.\,{15^2}.\,35 = 7875\pi \approx 24728\,\left( {c{m^3}} \right)\)
b) Thể tích nước mỗi lần xách là: \(24728\,.\,90\% = 22255\,\left( {c{m^3}} \right) = 0,022255\,\left( {{m^3}} \right)\).
Số thùng ít nhất cần đổ để đầy bể là:\(1\,\,:\,\,0,022255\,\, = \,\,44,9337..\) nên số thùng cần là \[45\] thùng
Lời giải
a) Các nhóm \[\left[ {70;80} \right),\,\,\left[ {80;90} \right),\,\,\left[ {90;100} \right),\,\,\left[ {100;110} \right),\,\,\left[ {110;120} \right).\]) có tần số lần lượt là: \[n{}_1\, = \,3\], , \[n{}_2\, = \,6\], \[{n_3}\, = \,12\], \[{n_4}\, = \,5\], \[n{}_5\, = \,4\].
b)
|
Nhóm |
Tần số \[\left( n \right)\] |
|
\[\left[ {70\,;\,80} \right)\] |
\[3\] |
|
\[\left[ {80\,;\,90} \right)\] |
\[6\] |
|
\[\left[ {90\,;\,100} \right)\] |
\[12\] |
|
\[\left[ {100\,;\,110} \right)\] |
\[5\] |
|
\[\left[ {110\,;\,120} \right)\] |
\[4\] |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.