Hai trường X và Y có 420 học sinh đậu vào lớp 10 đạt tỉ lệ 84%. Riêng trường X tỉ lệ đậu 80%, riêng trường Y tỉ lệ đậu 90%. Tính số học sinh dự thi của mỗi trường.
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 10 !!
Quảng cáo
Trả lời:
Tổng số học sinh dự thi của hai trường X và Y là: \(420:84\% = 500\)
Gọi \(x\), \(y\) lần lượt là số học sinh hai trường X và Y (\(x\); \(y\) nguyên dương, \(x\); \(y < 420\))
Vì số học sinh dự thi của 2 trường là 500 học sinh nên ta có phương trình \(x + y = 500\) \(\left( 1 \right)\)
Tỉ lệ đạu lớp 10 của riêng trường X là 80%, trường Y là 90% nên ta có phương trình: \(0,8x + 0,9y = 420\)\(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình:
\(\left\{ \begin{array}{l}x + y = 500\\0,8x + 0,9y = 420\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 300\\y = 200\end{array} \right.\) (thỏa mãn)
Vậy trường X có \(300\) học sinh tham gia dự thi và trường Y là\(200\) học sinh dự thi.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
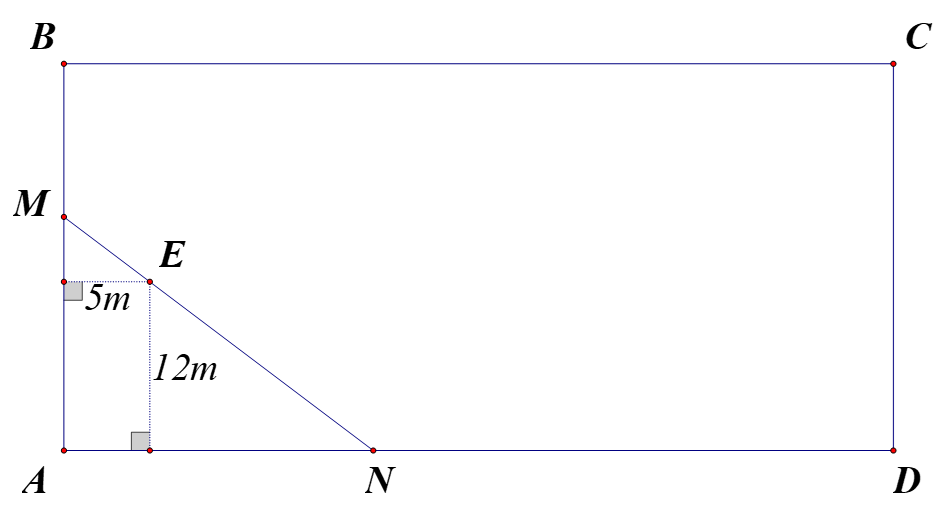
Gọi khoảng cách từ \(E\) đến \(AB,AD\) lần lượt là \(EH,EK.\)
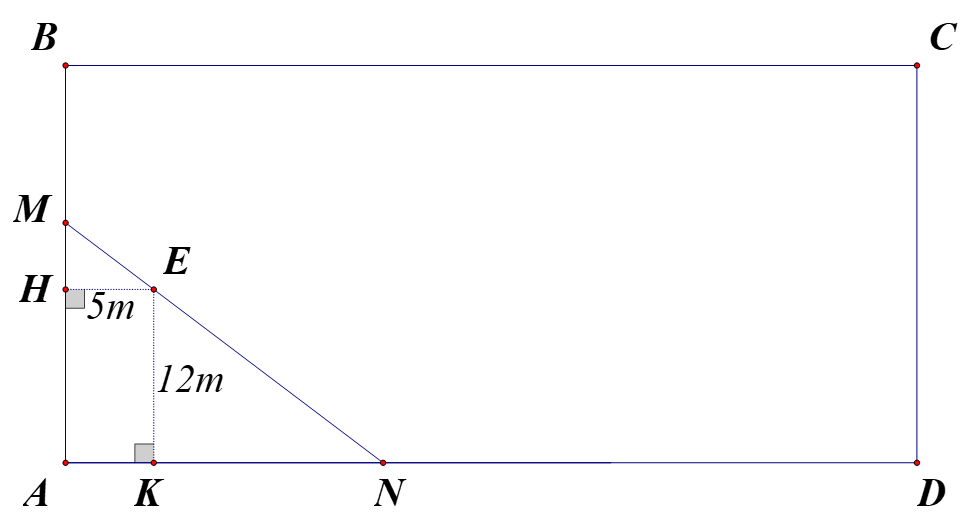
Đặt \(KN = x\left( m \right)\), đk: \(x > 0\)
Hai tam giác vuông \(KEN,HME\) đồng dạng nên \[\frac{{KE}}{{KN}} = \frac{{HM}}{{HE}} \Rightarrow \frac{{12}}{x} = \frac{{HM}}{5} \Rightarrow HM = \frac{{60}}{x}\left( m \right)\]
Diện tích tam giác \(AMN\) là:
\({S_{AMN}} = \frac{1}{2}.AM.AN = \frac{1}{2}.\left( {12 + \frac{{60}}{x}} \right).\left( {5 + x} \right) = \left( {6 + \frac{{30}}{x}} \right).\left( {5 + x} \right)\)
\[30 + 6x + \frac{{150}}{x} + 30 = 60 + 6x + \frac{{150}}{x} \ge 60 + 2\sqrt {6x.\frac{{150}}{x}} = \]120
Dấu “=” xảy ra khi
\[6x = \frac{{150}}{x}\]
\[{x^2} = 25\]
\[x = 5\].
Vậy diện tích nhỏ nhất của phần góc ao \(AMN\) mà anh Thịnh có thể quây được là \(120{m^2}\)..
Lời giải
a) Vì nhà bạn Trang sử dụng hết 25m3 nước nên số tiền nhà Trang phải trả là 10m3 theo giá ở bậc 1; 10m3 theo giá ở bậc hai; 5m3 theo giá ở bậc 3.
Số tiền nhà bạn Trang phải trả cho 10m3 nước đầu tiên là:
10.6000 = 60 000 (đồng)
Số tiền nhà bạn Trang phải trả cho 10m3 nước tiếp theo là:
10.7100 = 71 000 (đồng)
Số tiền nhà bạn Trang phải trả cho 5m3 nước tiếp theo nữa là:
5.8600 = 43 000 (đồng)
Vậy tổng số tiền nhà bạn Trang phải trả là:
60 000 + 71 000 + 43 000 = 174 000 (đồng)
b) Số tiền phải trả cho 30m3 nước đầu tiên là:
10.6000 + 10.7100 + 10.8600 = 217 000 (đồng)
Vì 297 000 (đồng) lớn hơn 217 000 (đồng) nên nhà Trang đã phải trả một số tiền theo giá ở bậc 4.
Gọi số mét khối nước mà nhà Trang phải trả theo giá ở bậc 4 là x (m3).
Theo đề bài ta có: 217 000 + x.16 000 = 297 000
Tìm được x = 5
Vậy trong tháng 2 nhà bạn Trang dùng hết 30 + 5 = 35 m3 nước
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.