(1,5 điểm)
Một khu vui chơi dành cho trẻ em thống kê lại độ tuổi của trẻ em đến chơi trong một ngày và lập được biểu đồ đoạn thẳng như sau:
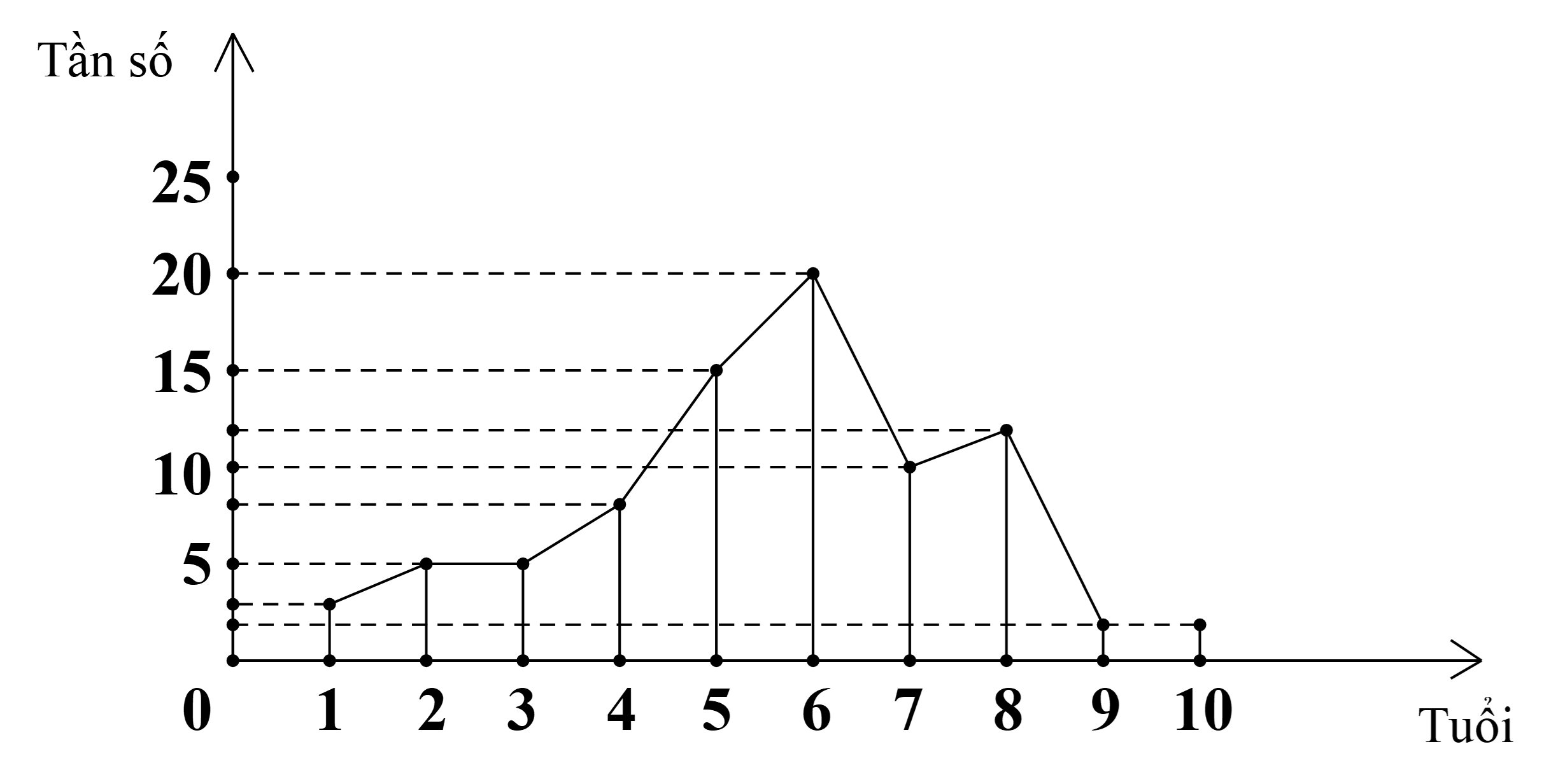
Quan sát biểu đồ cho biết: Trong các trẻ em đến khu vui chơi, trẻ em ở
Một khu vui chơi dành cho trẻ em thống kê lại độ tuổi của trẻ em đến chơi trong một ngày và lập được biểu đồ đoạn thẳng như sau:

Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 10 !!
Quảng cáo
Trả lời:
Câu hỏi cùng đoạn
Câu 2:
Một hộp chứa 10 quả bóng màu đỏ và một số quả bóng màu vàng (các quả bóng có khối lượng và kích thước như nhau). Lấy ra ngẫu nhiên một quả bóng trong hộp rồi thả lại hộp. Biết xác suất của biến cố: “Lấy được quả bóng màu đỏ” là 0,4. Hỏi trong hộp có bao nhiêu quả bóng màu vàng?
Một hộp chứa 10 quả bóng màu đỏ và một số quả bóng màu vàng (các quả bóng có khối lượng và kích thước như nhau). Lấy ra ngẫu nhiên một quả bóng trong hộp rồi thả lại hộp. Biết xác suất của biến cố: “Lấy được quả bóng màu đỏ” là 0,4. Hỏi trong hộp có bao nhiêu quả bóng màu vàng?
Gọi số quả bóng màu vàng là \(x\) (quả), đk: \(x \in {\mathbb{N}^*}\)
Tổng số bóng trong hộp là \(10 + x\) (quả)
Xác suất của biến cố “Lấy được quả bóng màu đỏ” là \(\frac{{10}}{{10 + x}}\)
Theo bài ra: \(\frac{{10}}{{10 + x}} = 0,4\) hay \(10 + x = 25 \Rightarrow x = 15\) (t/m)
Vậy có 15 quả bóng màu vàng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Tổng số học sinh dự thi của hai trường X và Y là: \(420:84\% = 500\)
Gọi \(x\), \(y\) lần lượt là số học sinh hai trường X và Y (\(x\); \(y\) nguyên dương, \(x\); \(y < 420\))
Vì số học sinh dự thi của 2 trường là 500 học sinh nên ta có phương trình \(x + y = 500\) \(\left( 1 \right)\)
Tỉ lệ đạu lớp 10 của riêng trường X là 80%, trường Y là 90% nên ta có phương trình: \(0,8x + 0,9y = 420\)\(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình:
\(\left\{ \begin{array}{l}x + y = 500\\0,8x + 0,9y = 420\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 300\\y = 200\end{array} \right.\) (thỏa mãn)
Vậy trường X có \(300\) học sinh tham gia dự thi và trường Y là\(200\) học sinh dự thi.
Lời giải
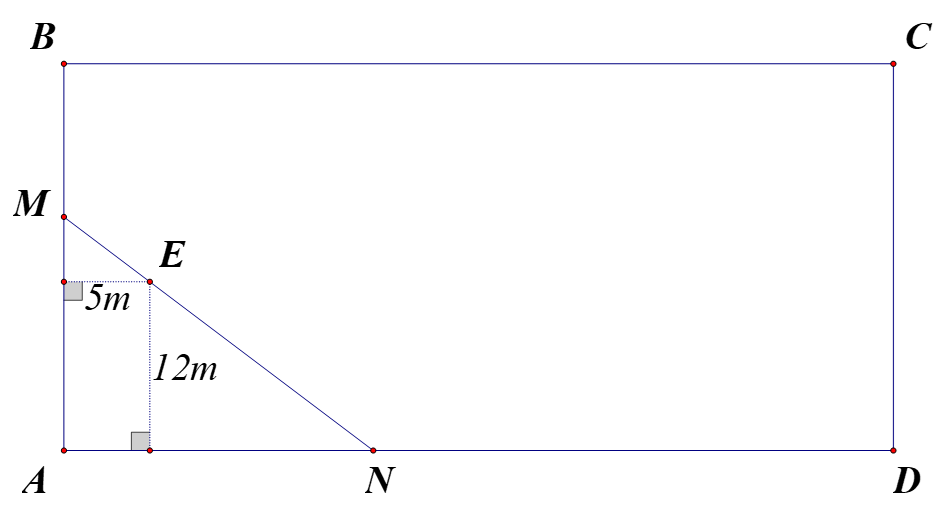
Gọi khoảng cách từ \(E\) đến \(AB,AD\) lần lượt là \(EH,EK.\)
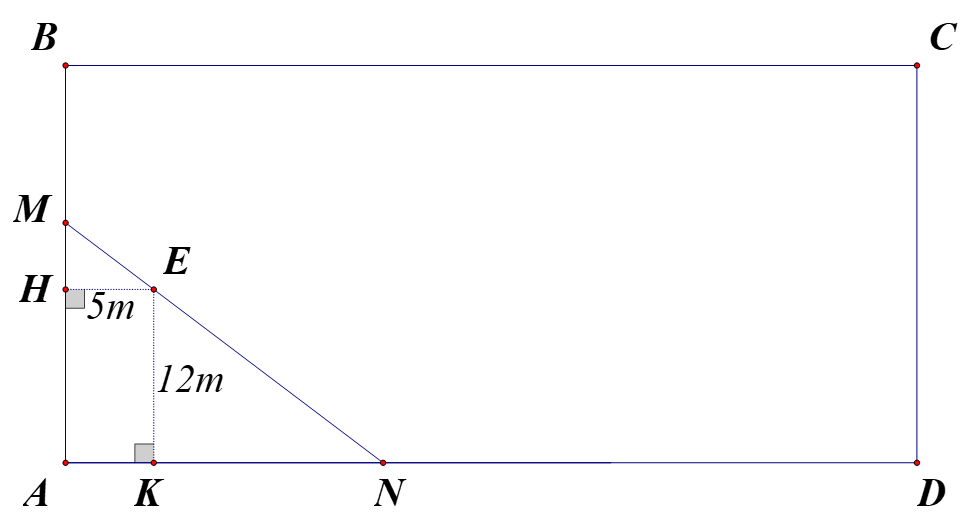
Đặt \(KN = x\left( m \right)\), đk: \(x > 0\)
Hai tam giác vuông \(KEN,HME\) đồng dạng nên \[\frac{{KE}}{{KN}} = \frac{{HM}}{{HE}} \Rightarrow \frac{{12}}{x} = \frac{{HM}}{5} \Rightarrow HM = \frac{{60}}{x}\left( m \right)\]
Diện tích tam giác \(AMN\) là:
\({S_{AMN}} = \frac{1}{2}.AM.AN = \frac{1}{2}.\left( {12 + \frac{{60}}{x}} \right).\left( {5 + x} \right) = \left( {6 + \frac{{30}}{x}} \right).\left( {5 + x} \right)\)
\[30 + 6x + \frac{{150}}{x} + 30 = 60 + 6x + \frac{{150}}{x} \ge 60 + 2\sqrt {6x.\frac{{150}}{x}} = \]120
Dấu “=” xảy ra khi
\[6x = \frac{{150}}{x}\]
\[{x^2} = 25\]
\[x = 5\].
Vậy diện tích nhỏ nhất của phần góc ao \(AMN\) mà anh Thịnh có thể quây được là \(120{m^2}\)..
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.