(2,5 điểm)
Trên địa bàn thành phố \(X\) có \(1850\) học sinh lớp \(9\) đăng kí dự thi tuyển sinh vào lớp \(10\) của hai trường THPT A và B, kết quả có 680 học sinh trúng tuyển. Biết tỉ lệ trúng tuyển của trường A là \(30\% \) và trường B là \(80\% \). Hỏi mỗi trường có bao nhiêu có bao nhiêu học sinh lớp \(9\) đăng kí dự thi vào lớp \(10\).
(2,5 điểm)
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 15 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Bài toán có thể được giải bằng cách lập hệ phương trình dựa trên thông tin đề bài:
Gọi \(x\) là số học sinh đăng ký dự thi vào trường A
Gọi \(y\) là số học sinh đăng ký dự thi vào trường B
Theo đề bài, ta có hệ phương trình sau:
+) Tổng số học sinh đăng ký dự thi là 1850 học sinh: \(x + y = 1850\)
+) Tổng số học sinh trúng tuyển là 680 học sinh. Số học sinh trúng tuyển tại trường A chiếm 30% số học sinh đăng ký vào trường A, và tại trường B chiếm 80% số học sinh đăng ký vào trường B: \(0,3x + 0,8y = 680\)
Giải hệ phương trình này, ta có:
\(\left\{ {\begin{array}{*{20}{l}}{x + y = 1850}\\{0,3x + 0,8y = 680}\end{array}} \right.\)
Từ phương trình thứ nhất, ta có:\(y = 1850 - x\)
Thay \(y = 1850 - x\) vào phương trình thứ hai ta được:
\(0,3x + 0,8(1850 - x) = 680\)
\(0,3x + 0,8 \cdot 1850 - 0,8x = 680\)
\(0,3x + 1480 - 0,8x = 680\)
\( - 0,5x + 1480 = 680\)
\( - 0,5x = 680 - 1480\)
\( - 0,5x = - 800\)
\(x = \frac{{ - 800}}{{ - 0,5}} = 1600\)
+) Tìm \(y = 1850 - 1600 = 250\)
Vậy số học sinh đăng ký dự thi vào:
- Trường A là 1600 học sinh.
- Trường B là 250 học sinh.
Câu hỏi cùng đoạn
Câu 2:
Sân vận động Quốc gia Mỹ Đình (Quận Nam Từ Liêm – Hà Nội) có mặt sân bóng hình chữ nhật với chiều dài hơn chiều rộng 37m và có diện tích là 7140\({m^2}\). Hãy tính chiều dài và chiều rộng của mặt sân bóng đá này.
Sân vận động Quốc gia Mỹ Đình (Quận Nam Từ Liêm – Hà Nội) có mặt sân bóng hình chữ nhật với chiều dài hơn chiều rộng 37m và có diện tích là 7140\({m^2}\). Hãy tính chiều dài và chiều rộng của mặt sân bóng đá này.
Giải bởi Vietjack
Gọi chiều rộng mặt sân là \(x(m)\) (\(x > 0\)) \( \Rightarrow \) chiều dài mặt sân là \(x + 37(m)\)
Vì diện tích mặt sân là 7140\({m^2}\) nên ta có phương trình:
\(x(x + 37) = 7140\)
\({x^2} + 37x - 7140 = 0\)
Giải phương trình, ta được: \(x = 68(tm)\); \(x = - 105(ktm)\)
Vậy chiều rộng mặt sân là 68, chiều dài là \(68 + 37 = 105m\).
Câu 3:
Tìm tất cả các giá trị của tham số \(m\) để phương trình \({x^2} - 2mx + 4m - 4 = 0\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(x_1^2 + x_2^2 - 8 = 0\).
Giải bởi Vietjack
Xét phương trình \({x^2} - 2mx + 4m - 4 = 0\)
Phương trình đã cho có hai nghiệm \({x_1},{x_2}\) khi
\(\Delta \prime > 0\)
\({m^2} - 4m + 4 > 0\)
\({(m - 2)^2} > 0\)
\(m - 2 \ne 0\)
\(m \ne 2\)
Với \(m \ne 2\) thì phương trình đã cho có hai nghiệm \({x_1},{x_2}\)
Áp dụng hệ thức Viète ta có: \({x_1} + {x_2} = \frac{{ - b}}{a} = 2m;{x_1}{x_2} = \frac{c}{a} = 4m - 4\)
Theo đề bài ta có:
\(x_1^2 + x_2^2 - 8 = 0\)
\({({x_1} + {x_2})^2} - 2{x_1}{x_2} - 8 = 0\)
\({(2m)^2} - 2.(4m - 4) - 8 = 0\)
\(4{m^2} - 8m + 8 - 8 = 0\)
\(4{m^2} - 8m = 0\)
\(4m(m - 2) = 0\)
\(4m = 0\) hoặc \(m - 2 = 0\)
\(m = 0\) (thỏa mãn điều kiện) hoặc \(m = 2\) (không thỏa mãn điều kiện)
Vậy \(m = 0\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a. Vì hộp sữa hình trụ có chiều cao \(h = 12cm\) và thể tích \(V = 192\pi c{m^3}\) nên:
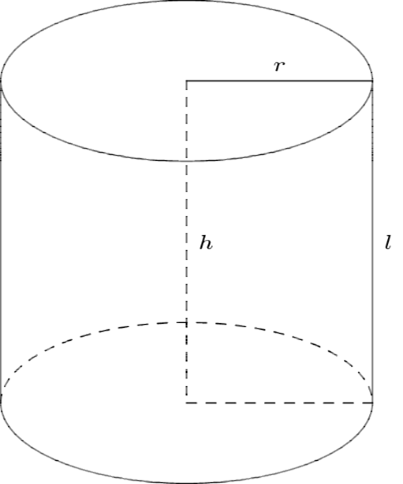
\(V = \pi {r^2}h\)
\(192\pi = 12\pi {r^2}\)
\({r^2} = 16\)
\( \Rightarrow r = 4cm\)
b. Vì hộp sữa hình trụ có \(r = 4cm\) và chiều cao \(h = 12cm\) nên diện tích toàn phần của hộp sữa là:
\({S_{tp}} = 2\pi r(h + r) = 2\pi .4(12 + 4) \approx 402,124(c{m^2}) \approx 0,04{m^2}\)
Chi phí sản xuất 10 000 vỏ hộp sữa là: \(0,04.10000.80000 = 32000000\) đồng
Lời giải
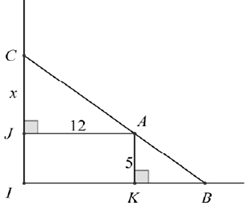
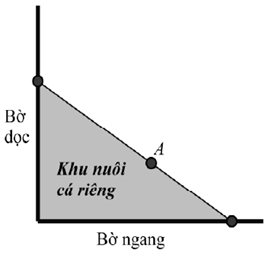
Đặt tên các điểm như hình vẽ. Đặt\(CJ = x,(x > 0).\)
Vì hai tam giác AJC và BKA là hai tam giác đồng dạng nên:
\(\frac{{CJ}}{{AK}} = \frac{{JA}}{{KB}}\)
\(\frac{x}{5} = \frac{{12}}{{KB}}\)
\(KB = \frac{{60}}{x}.\)
Diện tích của khu nuôi cá là:\(S = \frac{1}{2}\left( {x + 5} \right).\left( {\frac{{60}}{x} + 12} \right).\)
\(S(x) = \frac{1}{2}\left( {60 + 12x + \frac{{300}}{x} + 60} \right)\)
\(S(x) = 6x + \frac{{150}}{x} + 60\)
Áp dụng bất đẳng thức Cô si ta có:
\(6x + \frac{{150}}{x} \ge 2\sqrt {6x.\frac{{150}}{x}} = 60\)
Dấu bằng xảy ra khi \(6x = \frac{{150}}{x}\).
\({x^2} = 25\)
\(x = 5\)
Nên \(S(x) = 6x + \frac{{150}}{x} + 60 \ge 60 + 60 = 120\)
Suy ra diện tích nhỏ nhất có thể giăng là \(120({m^2})\), đạt được khi \(x = 5\,m\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
(1,5 điểm): Cho hai biểu thức: \(A = \frac{{\sqrt x }}{{\sqrt x + 2}}\) và \(B = \frac{2}{{\sqrt x - 1}} - \frac{{\sqrt x - 2}}{{x - \sqrt x }}\) với \(x > 0;x \ne 1\).
1) Tính giá trị của biểu thức \(A\) khi \(x = 4\).
2) Chứng minh \(B = \frac{{\sqrt x + 2}}{{x - \sqrt x }}\).
3) Xét biểu thức \(P = A + \frac{1}{B}\). Tìm \(x\)để \(P \ge 1\).
(1,5 điểm): Cho hai biểu thức: \(A = \frac{{\sqrt x }}{{\sqrt x + 2}}\) và \(B = \frac{2}{{\sqrt x - 1}} - \frac{{\sqrt x - 2}}{{x - \sqrt x }}\) với \(x > 0;x \ne 1\).
1) Tính giá trị của biểu thức \(A\) khi \(x = 4\).
2) Chứng minh \(B = \frac{{\sqrt x + 2}}{{x - \sqrt x }}\).
3) Xét biểu thức \(P = A + \frac{1}{B}\). Tìm \(x\)để \(P \ge 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập