Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 15
56 người thi tuần này 4.6 121 lượt thi 9 câu hỏi 120 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Đoạn văn 1
Lời giải
|
Số lượt nháy chuột |
\(0\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
|
Tần số tương đối |
\(22,73\% \) |
\(50,91\% \) |
\(10,91\% \) |
\(8,18\% \) |
\(4,54\% \) |
\(2,73\% \) |
Lời giải
Bước 1: Xác định không gian mẫu (S)
Không gian mẫu \(S\) là tất cả các kết quả có thể xảy ra khi lấy ngẫu nhiên một viên bi từ hộp. Vì hộp có 10 viên bi được đánh số từ 1 đến 10, nên:
\(S = \{ 1,2,3,4,5,6,7,8,9,10\} \)
Số phần tử của không gian mẫu là \(|S| = 10\).
Bước 2: Xác định biến cố \(A\)
Biến cố \(A\) là việc viên bi lấy ra có số ghi trên đó là số nguyên tố. Các số nguyên tố trong khoảng từ 1 đến 10 là:\(\{ 2,3,5,7\} \)
Vậy biến cố \(A\) là tập hợp:\(A = \{ 2,3,5,7\} \)
Số phần tử của biến cố \(A\) là \(|A| = 4\).
Bước 3: Tính xác suất của biến cố \(A\)
Xác suất của biến cố \(A\) được tính bằng tỉ số giữa số phần tử của biến cố \(A\) và số phần tử của không gian mẫu \(S\):
\(P(A) = \frac{{|A|}}{{|S|}} = \frac{4}{{10}} = \frac{2}{5}\)
Kết luận: Xác suất để lấy được một viên bi có số ghi trên đó là số nguyên tố là \(\frac{2}{5}\).
Câu 3
(1,5 điểm): Cho hai biểu thức: \(A = \frac{{\sqrt x }}{{\sqrt x + 2}}\) và \(B = \frac{2}{{\sqrt x - 1}} - \frac{{\sqrt x - 2}}{{x - \sqrt x }}\) với \(x > 0;x \ne 1\).
1) Tính giá trị của biểu thức \(A\) khi \(x = 4\).
2) Chứng minh \(B = \frac{{\sqrt x + 2}}{{x - \sqrt x }}\).
3) Xét biểu thức \(P = A + \frac{1}{B}\). Tìm \(x\)để \(P \ge 1\).
(1,5 điểm): Cho hai biểu thức: \(A = \frac{{\sqrt x }}{{\sqrt x + 2}}\) và \(B = \frac{2}{{\sqrt x - 1}} - \frac{{\sqrt x - 2}}{{x - \sqrt x }}\) với \(x > 0;x \ne 1\).
1) Tính giá trị của biểu thức \(A\) khi \(x = 4\).
2) Chứng minh \(B = \frac{{\sqrt x + 2}}{{x - \sqrt x }}\).
3) Xét biểu thức \(P = A + \frac{1}{B}\). Tìm \(x\)để \(P \ge 1\).
Lời giải
Biểu thức \(A\) được cho là: \(A = \frac{{\sqrt x }}{{\sqrt x + 2}}\)
Thay \(x = 4\) vào biểu thức:
\(A = \frac{{\sqrt 4 }}{{\sqrt 4 + 2}} = \frac{2}{4} = \frac{1}{2}\)
Vậy giá trị của \(A\) khi \(x = 4\) là \(\frac{1}{2}\).
2) Chứng minh \(B = \frac{{\sqrt x + 2}}{{x - \sqrt x }}\)
Biểu thức \(B\) được cho là:
\(B = \frac{2}{{\sqrt x - 1}} - \frac{{\sqrt x - 2}}{{x - \sqrt x }}\)
\(B = \frac{2}{{(\sqrt x - 1)}} - \frac{{\sqrt x - 2}}{{\sqrt x (\sqrt x - 1)}}\)
\(B = \frac{{2\sqrt x }}{{\sqrt x (\sqrt x - 1)}} - \frac{{\sqrt x - 2}}{{\sqrt x (\sqrt x - 1)}}\)
\(B = \frac{{2\sqrt x - \sqrt x + 2}}{{(\sqrt x - 1)(\sqrt x - 1)}}\)
\(B = \frac{{\sqrt x + 2}}{{x - \sqrt x }}\)
Điều phải chứng minh
3) Ta có: \(P = A + \frac{1}{B} = \frac{{\sqrt x }}{{\sqrt x + 2}} + \frac{{x - \sqrt x }}{{\sqrt x + 2}} = \frac{x}{{\sqrt x + 2}}\) với
\(P = \frac{x}{{\sqrt x + 2}} \ge 1 \Rightarrow x \ge \sqrt x + 2 \Rightarrow x - \sqrt x - 2 \ge 0\)
\( \Rightarrow \left( {\sqrt x + 1} \right)\left( {\sqrt x - 2} \right) \ge 0\)
\(\left( {\sqrt x - 2} \right) \ge 0\)
\(\sqrt x \ge 2\)
\( \Rightarrow x \ge 4\)
Kết hợp với điều kiện ta đc \(x \ge 4\) thì \(P \ge 1\)
Lời giải
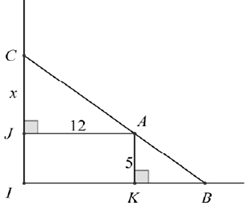
Đặt tên các điểm như hình vẽ. Đặt\(CJ = x,(x > 0).\)
Vì hai tam giác AJC và BKA là hai tam giác đồng dạng nên:
\(\frac{{CJ}}{{AK}} = \frac{{JA}}{{KB}}\)
\(\frac{x}{5} = \frac{{12}}{{KB}}\)
\(KB = \frac{{60}}{x}.\)
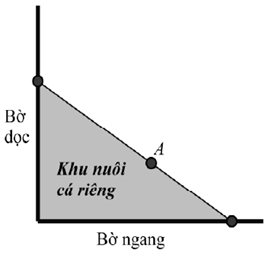
Diện tích của khu nuôi cá là:\(S = \frac{1}{2}\left( {x + 5} \right).\left( {\frac{{60}}{x} + 12} \right).\)
\(S(x) = \frac{1}{2}\left( {60 + 12x + \frac{{300}}{x} + 60} \right)\)
\(S(x) = 6x + \frac{{150}}{x} + 60\)
Áp dụng bất đẳng thức Cô si ta có:
\(6x + \frac{{150}}{x} \ge 2\sqrt {6x.\frac{{150}}{x}} = 60\)
Dấu bằng xảy ra khi \(6x = \frac{{150}}{x}\).
\({x^2} = 25\)
\(x = 5\)
Nên \(S(x) = 6x + \frac{{150}}{x} + 60 \ge 60 + 60 = 120\)
Suy ra diện tích nhỏ nhất có thể giăng là \(120({m^2})\), đạt được khi \(x = 5\,m\).
Đoạn văn 2
Lời giải
Bài toán có thể được giải bằng cách lập hệ phương trình dựa trên thông tin đề bài:
Gọi \(x\) là số học sinh đăng ký dự thi vào trường A
Gọi \(y\) là số học sinh đăng ký dự thi vào trường B
Theo đề bài, ta có hệ phương trình sau:
+) Tổng số học sinh đăng ký dự thi là 1850 học sinh: \(x + y = 1850\)
+) Tổng số học sinh trúng tuyển là 680 học sinh. Số học sinh trúng tuyển tại trường A chiếm 30% số học sinh đăng ký vào trường A, và tại trường B chiếm 80% số học sinh đăng ký vào trường B: \(0,3x + 0,8y = 680\)
Giải hệ phương trình này, ta có:
\(\left\{ {\begin{array}{*{20}{l}}{x + y = 1850}\\{0,3x + 0,8y = 680}\end{array}} \right.\)
Từ phương trình thứ nhất, ta có:\(y = 1850 - x\)
Thay \(y = 1850 - x\) vào phương trình thứ hai ta được:
\(0,3x + 0,8(1850 - x) = 680\)
\(0,3x + 0,8 \cdot 1850 - 0,8x = 680\)
\(0,3x + 1480 - 0,8x = 680\)
\( - 0,5x + 1480 = 680\)
\( - 0,5x = 680 - 1480\)
\( - 0,5x = - 800\)
\(x = \frac{{ - 800}}{{ - 0,5}} = 1600\)
+) Tìm \(y = 1850 - 1600 = 250\)
Vậy số học sinh đăng ký dự thi vào:
- Trường A là 1600 học sinh.
- Trường B là 250 học sinh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.