(4,0 điểm)
Một doanh nghiệp sản xuất vỏ hộp sữa ông thọ dạng hình trụ (như hình minh họa bên dưới), có chiều cao bằng \(12\,cm\). Biết thể tích của hộp là\(192\pi \,c{m^3}\).
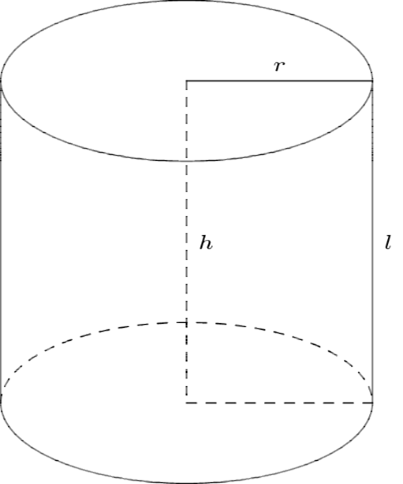
a). Tính bán kính đáy của hình trụ
b) Tính số tiền mà doanh nghiệp cần chi để sản xuất \(10\,000\)vỏ hộp sữa ông thọ (kể cả hai nắp hộp), biết chi phí để sản xuất vỏ hộp đó là \(80\,000\) đồng/m2 (làm tròn kết quả đến phần ngàn).
Một doanh nghiệp sản xuất vỏ hộp sữa ông thọ dạng hình trụ (như hình minh họa bên dưới), có chiều cao bằng \(12\,cm\). Biết thể tích của hộp là\(192\pi \,c{m^3}\).
a). Tính bán kính đáy của hình trụ
b) Tính số tiền mà doanh nghiệp cần chi để sản xuất \(10\,000\)vỏ hộp sữa ông thọ (kể cả hai nắp hộp), biết chi phí để sản xuất vỏ hộp đó là \(80\,000\) đồng/m2 (làm tròn kết quả đến phần ngàn).
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 15 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
\(V = \pi {r^2}h\)
\(192\pi = 12\pi {r^2}\)
\({r^2} = 16\)
\( \Rightarrow r = 4cm\)
b. Vì hộp sữa hình trụ có \(r = 4cm\) và chiều cao \(h = 12cm\) nên diện tích toàn phần của hộp sữa là:
\({S_{tp}} = 2\pi r(h + r) = 2\pi .4(12 + 4) \approx 402,124(c{m^2}) \approx 0,04{m^2}\)
Chi phí sản xuất 10 000 vỏ hộp sữa là: \(0,04.10000.80000 = 32000000\) đồng
Câu hỏi cùng đoạn
Câu 2:
Cho đường tròn \((O;R)\) đường kính \(AB\). Kẻ tiếp tuyến \(Ax\), lấy \(P\) trên \(Ax\) (\(AP > R\)). Từ \(P\) kẻ tiếp tuyến \(PM\) với \((O)\).
a) Chứng minh rằng bốn điểm \(A,P,M,O\) cùng thuộc 1 đường tròn.
b) Chứng minh: \(BM//OP\). Đường thẳng vuông góc với \(AB\) tại \(O\) cắt tia \(BM\) tại \(N\). Chứng minh tứ giác \(OBNP\) là hình bình hành.
c) Giả sử \(AN\) cắt \(OP\) tại \(K;PM\) cắt \(ON\) tại \(I;PN\) cắt \(OM\) tại \(J\). Chứng minh \(I,J,K\) thẳng hàng.
Cho đường tròn \((O;R)\) đường kính \(AB\). Kẻ tiếp tuyến \(Ax\), lấy \(P\) trên \(Ax\) (\(AP > R\)). Từ \(P\) kẻ tiếp tuyến \(PM\) với \((O)\).
a) Chứng minh rằng bốn điểm \(A,P,M,O\) cùng thuộc 1 đường tròn.
b) Chứng minh: \(BM//OP\). Đường thẳng vuông góc với \(AB\) tại \(O\) cắt tia \(BM\) tại \(N\). Chứng minh tứ giác \(OBNP\) là hình bình hành.
c) Giả sử \(AN\) cắt \(OP\) tại \(K;PM\) cắt \(ON\) tại \(I;PN\) cắt \(OM\) tại \(J\). Chứng minh \(I,J,K\) thẳng hàng.
Giải bởi Vietjack
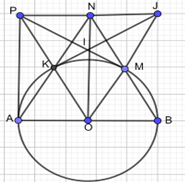
a) \(A,P,M,O\) cùng nằm trên đường tròn đường kính \(PO\)
b) Ta có: \(OP \bot AM;BM \bot AM \Rightarrow BM//OP\)
c) \(\Delta A{\rm{O}}P = \Delta OBN \Rightarrow OP = BN\), ta lại có \(BN//OP\) nên \(OPNB\) là hình bình hành
d) Ta có: \(ON \bot PJ;PM \bot OJ\), mà \(PM \bot ON = I \Rightarrow I\)là trực tâm \(\Delta POJ \Rightarrow IJ \bot OP\) (1)
Chứng minh được \(PAON\) là hình chữ nhật \( \Rightarrow K\) là trung điểm \(OP\)
Lại có: \(APO = OPI = IOP \Rightarrow AIPO\) cân tại \(I \Rightarrow IK \bot OP\) (2)
Từ (1)(2)\( \Rightarrow I,J,K\) thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bài toán có thể được giải bằng cách lập hệ phương trình dựa trên thông tin đề bài:
Gọi \(x\) là số học sinh đăng ký dự thi vào trường A
Gọi \(y\) là số học sinh đăng ký dự thi vào trường B
Theo đề bài, ta có hệ phương trình sau:
+) Tổng số học sinh đăng ký dự thi là 1850 học sinh: \(x + y = 1850\)
+) Tổng số học sinh trúng tuyển là 680 học sinh. Số học sinh trúng tuyển tại trường A chiếm 30% số học sinh đăng ký vào trường A, và tại trường B chiếm 80% số học sinh đăng ký vào trường B: \(0,3x + 0,8y = 680\)
Giải hệ phương trình này, ta có:
\(\left\{ {\begin{array}{*{20}{l}}{x + y = 1850}\\{0,3x + 0,8y = 680}\end{array}} \right.\)
Từ phương trình thứ nhất, ta có:\(y = 1850 - x\)
Thay \(y = 1850 - x\) vào phương trình thứ hai ta được:
\(0,3x + 0,8(1850 - x) = 680\)
\(0,3x + 0,8 \cdot 1850 - 0,8x = 680\)
\(0,3x + 1480 - 0,8x = 680\)
\( - 0,5x + 1480 = 680\)
\( - 0,5x = 680 - 1480\)
\( - 0,5x = - 800\)
\(x = \frac{{ - 800}}{{ - 0,5}} = 1600\)
+) Tìm \(y = 1850 - 1600 = 250\)
Vậy số học sinh đăng ký dự thi vào:
- Trường A là 1600 học sinh.
- Trường B là 250 học sinh.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
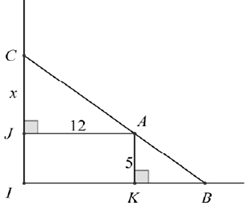
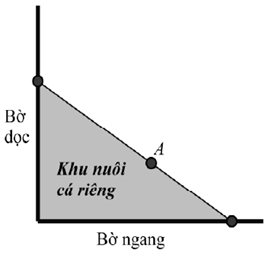
Đặt tên các điểm như hình vẽ. Đặt\(CJ = x,(x > 0).\)
Vì hai tam giác AJC và BKA là hai tam giác đồng dạng nên:
\(\frac{{CJ}}{{AK}} = \frac{{JA}}{{KB}}\)
\(\frac{x}{5} = \frac{{12}}{{KB}}\)
\(KB = \frac{{60}}{x}.\)
Diện tích của khu nuôi cá là:\(S = \frac{1}{2}\left( {x + 5} \right).\left( {\frac{{60}}{x} + 12} \right).\)
\(S(x) = \frac{1}{2}\left( {60 + 12x + \frac{{300}}{x} + 60} \right)\)
\(S(x) = 6x + \frac{{150}}{x} + 60\)
Áp dụng bất đẳng thức Cô si ta có:
\(6x + \frac{{150}}{x} \ge 2\sqrt {6x.\frac{{150}}{x}} = 60\)
Dấu bằng xảy ra khi \(6x = \frac{{150}}{x}\).
\({x^2} = 25\)
\(x = 5\)
Nên \(S(x) = 6x + \frac{{150}}{x} + 60 \ge 60 + 60 = 120\)
Suy ra diện tích nhỏ nhất có thể giăng là \(120({m^2})\), đạt được khi \(x = 5\,m\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
(1,5 điểm): Cho hai biểu thức: \(A = \frac{{\sqrt x }}{{\sqrt x + 2}}\) và \(B = \frac{2}{{\sqrt x - 1}} - \frac{{\sqrt x - 2}}{{x - \sqrt x }}\) với \(x > 0;x \ne 1\).
1) Tính giá trị của biểu thức \(A\) khi \(x = 4\).
2) Chứng minh \(B = \frac{{\sqrt x + 2}}{{x - \sqrt x }}\).
3) Xét biểu thức \(P = A + \frac{1}{B}\). Tìm \(x\)để \(P \ge 1\).
(1,5 điểm): Cho hai biểu thức: \(A = \frac{{\sqrt x }}{{\sqrt x + 2}}\) và \(B = \frac{2}{{\sqrt x - 1}} - \frac{{\sqrt x - 2}}{{x - \sqrt x }}\) với \(x > 0;x \ne 1\).
1) Tính giá trị của biểu thức \(A\) khi \(x = 4\).
2) Chứng minh \(B = \frac{{\sqrt x + 2}}{{x - \sqrt x }}\).
3) Xét biểu thức \(P = A + \frac{1}{B}\). Tìm \(x\)để \(P \ge 1\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập