(0,5 điểm) Công ty vàng bạc đá quý muốn làm một món đồ trang sức có hình hai hình cầu bằng nhau giao nhau như hình vẽ. Khối cầu có bán kính \[25cm\] khoảng cách giữa hai tâm hình cầu là \[40cm\]. Giá mạ vàng \[1{m^2}\] là \[4\,\,700\,\,000\] đồng. Nhà sản xuất muốn mạ vàng xung quanh món đồ trang sức đó. Tính số tiền cần dùng để mạ vàng khối trang sức đó.
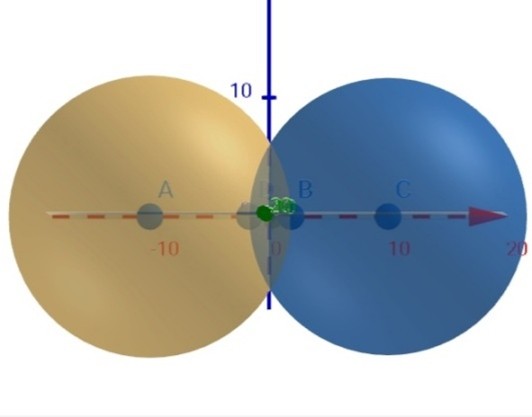
(0,5 điểm) Công ty vàng bạc đá quý muốn làm một món đồ trang sức có hình hai hình cầu bằng nhau giao nhau như hình vẽ. Khối cầu có bán kính \[25cm\] khoảng cách giữa hai tâm hình cầu là \[40cm\]. Giá mạ vàng \[1{m^2}\] là \[4\,\,700\,\,000\] đồng. Nhà sản xuất muốn mạ vàng xung quanh món đồ trang sức đó. Tính số tiền cần dùng để mạ vàng khối trang sức đó.
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 20 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
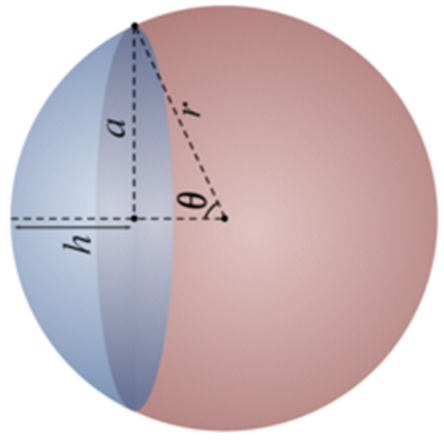
(Phần màu nhạt là phần giao nhau của hai khối cầu)
Gọi h là chiều cao của chỏm cầu. Ta có \[h = \frac{{2R - d}}{2} = \frac{{2.25 - 40}}{2} = 5cm\]
(\[d\]là khoảng cách giữa hai tâm)
Diện tích xung quanh của chỏm cầu là:\[{S_{xq}} = 2\pi Rh\]
Vì 2 khối cầu bằng nhau nên 2 hình chỏm cầu bằng nhau.
\[{S_{xq}}\] khối trang sức \[ = 2{S_{xq}}\] khối cầu\[ - 2{S_{xq}}\] chỏm cầu.
Khối trang sức có \[{S_{xq}} = 2.4\pi {R^2} - 2.2\pi Rh = 2.4\pi {.25^2} - 2.2\pi .25.5 = 4500\pi c{m^2} = 0.45{m^2}\]
Vậy số tiền dùng để mạ vàng khối trang sức đó là \[4700000.0,45\pi \approx 6640000\]đồng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
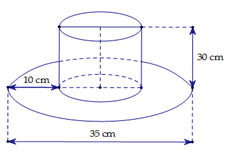
a) Bán kính hình trụ của cái mũ là \(r = \frac{{35 - 10 - 10}}{2} = \frac{{15}}{2}\;\left( {cm} \right)\).
Đường cao hình trụ của cái mũ là \(30\;cm\).
Diện tích xung hình trụ là: \({S_{xq}} = 2\pi rl = 2.\pi .\frac{{15}}{2}.30 = 450\pi \;\left( {c{m^2}} \right)\).
Diện tích vành mũ là: \({S_v} = \pi {\left( {\frac{{35}}{2}} \right)^2} - \pi {\left( {\frac{{15}}{2}} \right)^2} = 250\pi \left( {c{m^2}} \right)\).
Vậy tổng diện tích vải cần có để làm nên cái mũ đó (không tính phần viền, mép dán) là:
\(S = {S_{xq}} + {S_v} = 450\pi + 250\pi = 200\pi \approx \;628,32\left( {c{m^2}} \right)\).
b) thể tích phần có dạng hình nón của chiếc mũ là
\[V = \pi {r^2}h = \pi {\left( {\frac{{15}}{2}} \right)^2}.30 = \frac{{3375}}{2}\pi \approx 5301,44\left( {c{m^3}} \right)\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Tổng giá tiền theo niêm yết là 750 nghìn đồng nên ta có PT
\(x + y = 70\) (1)
Giá quyển từ điển được giảm 20% nên còn \(x - 20\% x = 0,8x\)(nghìn đồng);
Giá món đồ chơi được giảm 10%. nên còn \(y - 10\% y = 0,9y\)(nghìn đồng)
Do đó Bình chỉ phải trả 630 nghìn đồng nên ta có PT:
\(0,8x + 0,9y = 630\)(2)
Từ (1) và (2) ta có hệ PT
\(\left\{ \begin{array}{l}x + y = 750\\0,8{\rm{x}} + 0,9y = 630\end{array} \right.\)
Giải HPT được x = 450; y = 300( TMĐK)
Vậy giá quyển từ điển là 0,8. 450 = 360 (nghìn đồng)
Giá món đồ chơi là 0,9. 300 = 270 (nghìn đồng)
Câu 3
1) Công ty điện lực thống kê lượng điện tiêu thụ (đơn vị: kWh) cúa một số hộ gia đinh trong một khu vực trong tháng. Dữ liệu được ghi lại như sau:
150
120
180
200
130
100
160
190
219
210
170
140
110
130
160
180
150
200
210
190
Lâp bảng tần số ghép nhóm theo các khoảng lương điện tiêu thụ sau: \(\left[ {100;130} \right)\); \(\left[ {130;160} \right)\); Lời \(\left[ {160;190} \right)\); \(\left[ {190;220} \right)\).
1) Công ty điện lực thống kê lượng điện tiêu thụ (đơn vị: kWh) cúa một số hộ gia đinh trong một khu vực trong tháng. Dữ liệu được ghi lại như sau:
|
150 |
120 |
180 |
200 |
130 |
100 |
160 |
190 |
219 |
210 |
|
170 |
140 |
110 |
130 |
160 |
180 |
150 |
200 |
210 |
190 |
Lâp bảng tần số ghép nhóm theo các khoảng lương điện tiêu thụ sau: \(\left[ {100;130} \right)\); \(\left[ {130;160} \right)\); Lời \(\left[ {160;190} \right)\); \(\left[ {190;220} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập