Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 20
70 người thi tuần này 4.6 138 lượt thi 9 câu hỏi 120 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Đoạn văn 1
Câu 1
1) Công ty điện lực thống kê lượng điện tiêu thụ (đơn vị: kWh) cúa một số hộ gia đinh trong một khu vực trong tháng. Dữ liệu được ghi lại như sau:
150
120
180
200
130
100
160
190
219
210
170
140
110
130
160
180
150
200
210
190
Lâp bảng tần số ghép nhóm theo các khoảng lương điện tiêu thụ sau: \(\left[ {100;130} \right)\); \(\left[ {130;160} \right)\); Lời \(\left[ {160;190} \right)\); \(\left[ {190;220} \right)\).
1) Công ty điện lực thống kê lượng điện tiêu thụ (đơn vị: kWh) cúa một số hộ gia đinh trong một khu vực trong tháng. Dữ liệu được ghi lại như sau:
|
150 |
120 |
180 |
200 |
130 |
100 |
160 |
190 |
219 |
210 |
|
170 |
140 |
110 |
130 |
160 |
180 |
150 |
200 |
210 |
190 |
Lâp bảng tần số ghép nhóm theo các khoảng lương điện tiêu thụ sau: \(\left[ {100;130} \right)\); \(\left[ {130;160} \right)\); Lời \(\left[ {160;190} \right)\); \(\left[ {190;220} \right)\).
Lời giải
Bảng tần số ghép nhóm cho lượng điện tiêu thụ của hộ gia đình (đơn vị: kWh)
|
Khoảng lượng điện |
\(\left[ {100;130} \right)\) |
\(\left[ {130;160} \right)\) |
\(\left[ {160;190} \right)\) |
\(\left[ {190;220} \right)\) |
|
Tần số |
\[3\] |
\[5\] |
\[5\] |
\[7\] |
Lời giải
Không gian mẫu: \(\Omega = \){(2;3); (2;5); (2;8); (3;2); (3; 5); (3;8); (5;2); (5; 3); (5; 8); (8;2); (8;3); (8; 5)}. Có 12 phần tử.
Tích của các số ghi trên 2 tấm thẻ là số lẻ có 2 trường hợp là (3; 5); (5; 3)
Vậy \(P(M) = \frac{2}{{12}} = \frac{1}{6}\)
Lời giải
1) Thay \(x = 9\left( {TM} \right)\) vào biểu thức A, ta có:
\(A = \frac{{\sqrt 9 + 4}}{{\sqrt 9 - 1}} = \frac{{3 + 4}}{{3 - 1}} = \frac{7}{2}\)
Vậy \(A = \frac{7}{2}\) tại \(x = 9\).
2) Ta có \(B = \frac{{3\sqrt x + 1}}{{x + 2\sqrt x - 3}} - \frac{2}{{\sqrt x + 3}}\)với \(x \ge 0,\,x \ne 1\).\(\frac{A}{B} = \frac{x}{4} + 5\)
\(\begin{array}{l}B = \frac{{3\sqrt x + 1}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 1} \right)}} - \frac{2}{{\sqrt x + 3}}\\B = \frac{{3\sqrt x + 1}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 1} \right)}} - \frac{{2\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 1} \right)}}\\B = \frac{{3\sqrt x + 1}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 1} \right)}} - \frac{{2\sqrt x - 2}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 1} \right)}}\\B = \frac{{3\sqrt x + 1 - 2\sqrt x + 2}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 1} \right)}}\\B = \frac{{\sqrt x + 3}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 1} \right)}} = \frac{1}{{\sqrt x - 1}}\end{array}\)
3) Ta có \(\frac{A}{B} = \frac{{\sqrt x + 4}}{{\sqrt x - 1}}:\frac{1}{{\sqrt x - 1}} = \frac{{\sqrt x + 4}}{{\sqrt x - 1}}.\frac{{\sqrt x - 1}}{1} = \sqrt x + 4\)
Để
\(\begin{array}{l}\frac{A}{B} = \frac{x}{4} + 5\\ \Rightarrow \sqrt x + 4 = \frac{x}{4} + 5\\4\sqrt x + 16 = x + 20\\x - 4\sqrt x + 4 = 0\\\sqrt x = 2 \Leftrightarrow x = 4\left( {TM} \right)\end{array}\)
Vậy để \(\frac{A}{B} = \frac{x}{4} + 5\) thì \(x = 4\).
Lời giải
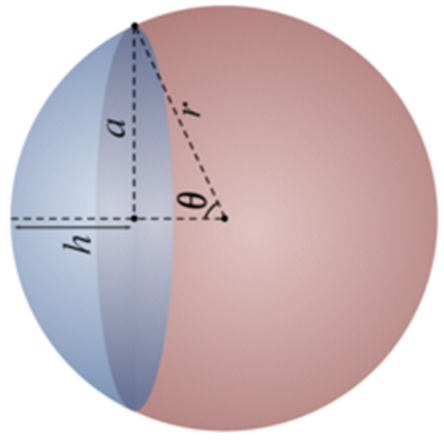
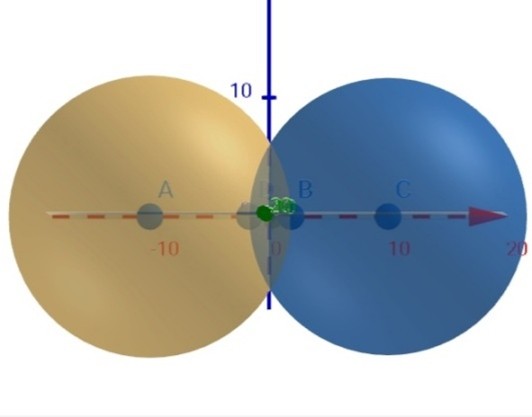
(Phần màu nhạt là phần giao nhau của hai khối cầu)
Gọi h là chiều cao của chỏm cầu. Ta có \[h = \frac{{2R - d}}{2} = \frac{{2.25 - 40}}{2} = 5cm\]
(\[d\]là khoảng cách giữa hai tâm)
Diện tích xung quanh của chỏm cầu là:\[{S_{xq}} = 2\pi Rh\]
Vì 2 khối cầu bằng nhau nên 2 hình chỏm cầu bằng nhau.
\[{S_{xq}}\] khối trang sức \[ = 2{S_{xq}}\] khối cầu\[ - 2{S_{xq}}\] chỏm cầu.
Khối trang sức có \[{S_{xq}} = 2.4\pi {R^2} - 2.2\pi Rh = 2.4\pi {.25^2} - 2.2\pi .25.5 = 4500\pi c{m^2} = 0.45{m^2}\]
Vậy số tiền dùng để mạ vàng khối trang sức đó là \[4700000.0,45\pi \approx 6640000\]đồng.
Đoạn văn 2
Lời giải
Tổng giá tiền theo niêm yết là 750 nghìn đồng nên ta có PT
\(x + y = 70\) (1)
Giá quyển từ điển được giảm 20% nên còn \(x - 20\% x = 0,8x\)(nghìn đồng);
Giá món đồ chơi được giảm 10%. nên còn \(y - 10\% y = 0,9y\)(nghìn đồng)
Do đó Bình chỉ phải trả 630 nghìn đồng nên ta có PT:
\(0,8x + 0,9y = 630\)(2)
Từ (1) và (2) ta có hệ PT
\(\left\{ \begin{array}{l}x + y = 750\\0,8{\rm{x}} + 0,9y = 630\end{array} \right.\)
Giải HPT được x = 450; y = 300( TMĐK)
Vậy giá quyển từ điển là 0,8. 450 = 360 (nghìn đồng)
Giá món đồ chơi là 0,9. 300 = 270 (nghìn đồng)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.